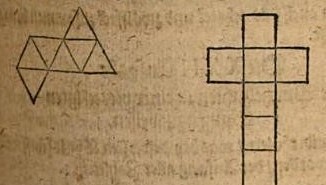| The Public Paperfolding History Project
Last updated 23/1/2024 x |
|||||||
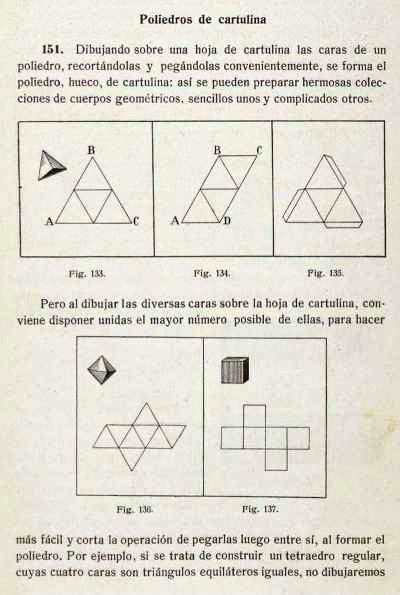
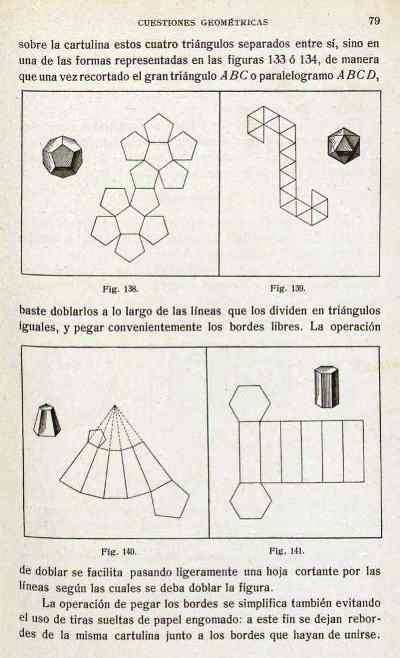
| Polyhedra constructed from irregular nets | |||||||
| This
page is being used to record information about the
history of Polyhedra constructed from irregular nets.
Please contact me if you know any of this information is
incorrect or if you have any other information that
should be added. Thank you. Note that this page is complete until 1882 but incomplete thereafter. ********** 1509 According to Max Stech in his book 'Dürers Gestaltlehre der Mathematik und der bildenden Künste (Dürer's Gestalt Theory of Mathematics and the Fine Arts), published by Halle an der Saale in 1948, a 1509 Venetian edition of 'Divina Proportione' by Luca Pacioli and illustrated by Leonardo da Vinci contains a drawing showing the foldable net of a regular dodecahedron. (Information from 'A History of Folding in Mathematics by Michael Freedman, published by Birkhauser in 2018.) I have not been able to verify this information.
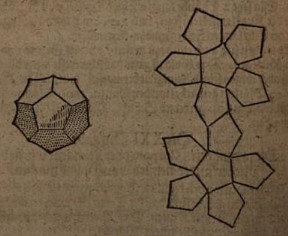
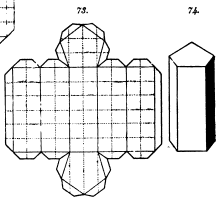
********** Charles de Bovelles (variously also known as Carolus or Bovillus) book 'Libellus de Matematicis Corporibus', published in 1510, included drawings of polyhedral nets for an icosahedron ( in three parts) and a fifteen sided solid constructed by adding pyramids to the pentagonal faces of a pentagonal prism. (Information from 'A History of Folding in Mathematics by Michael Freedman, published by Birkhauser in 2018.) I been not able to verify this information. ********** 1525 The fourth book of Albrecht Durer's 'Underweysung der Messung', published in 1525, contained foldable polyhedral nets for the five platonic solids, the truncated tetrahedron, the cuboctahedron, the truncated octahedron, the truncated cube, the rhombicuboctahedron, the truncated cuboctahedron, the snub cube and an eighteen sided solid made by adding pyramids to both hexagonal faces of a hexagonal prism. A revised edition, published in 1538, also included nets for the truncated icosahedron and the icosidodecahedron. (Information from 'A History of Folding in Mathematics by Michael Freedman, published by Birkhauser in 2018.)
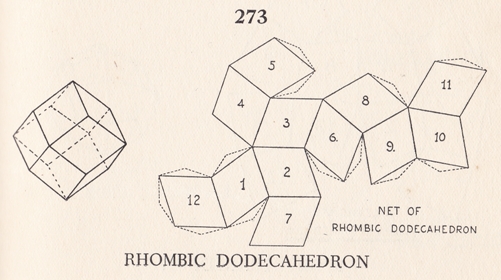
********** Cut and Fold Polyhedral Nets also appear in: 1636 Deliciae physico mathematicae oder mathematische und philosophische Erquickstunden' by Daniel Schwenter, which was published in Nürnberg in 1636, contained a net for the Rhombic Dodecahedron and a half net for the Triacontahedron.
********** 1651 Volume 2 of 'Deliciae physico mathematicae' written by Georg Phillip Harsdorffer, and published in 1651 gave cut and fold nets for the cube, octahedron and dodecahedron.
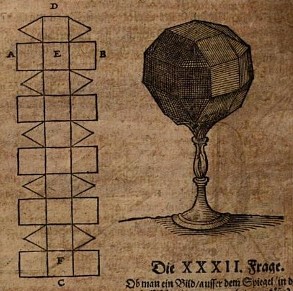
********** 1653 Volume 3 of 'Deliciae physico mathematicae' written by Georg Phillip Harsdorffer, and published in 1653 gave a net for the rhombicuboctahedron (although the net is incorrect as it is ten segments, rather than just eight, in height).
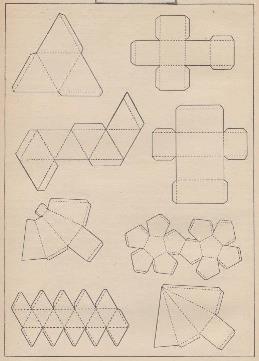
.********** 1872 'Das Deutschen Knaben Handwerksbusch' by Barth and Niederley, which was published in Bielefield and Leipzig in 1872. ********** 1882 Part Two of 'The Kindergarten Guide' by Maria Kraus Boelte and John Kraus, which was probably first published by E. Steiger and Company in New York in 1882, contains nets for what are termed 'Crystals' but are in fact for various prisms and pyramids, all the Platonic solids, a truncated square-based pyramid, a cone and a cylinder.
********** 1895 Eleonore Heerwart's 'Course in Paperfolding', which was first published in Dutch in 1895 then in English by Charles and Dible in London and Glasgow in 1896.
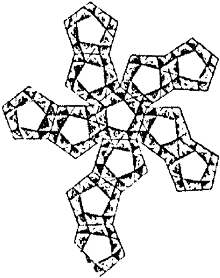
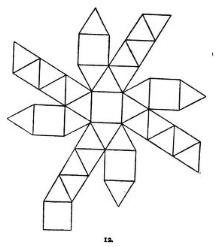
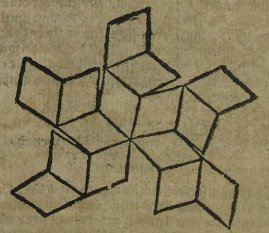
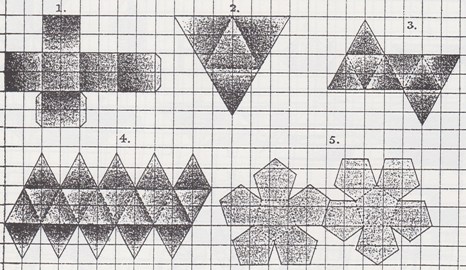
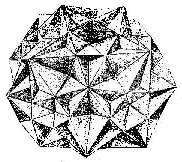
********** 1903 'La Ensenanza del Trabajo Manuel' by Pedro de Alcántara García and Teodosio Leal y Quiroga, which was published in Madrid in 1903, contains nets, or in some cases partial nets, for creating the tetrahedron, the stellated tetrahedron, the cube, the octahedron, the compound of five tetrahedra, the dodecahedron, the icosahedron, a polyhedron which will wrap the combination of seven cubes, and the three complex compound polyhedra also shown below.
********** 1918 'Ciencia Recreativa' by Jose Estralella, which was published by Gustavo Gili in Barcelona in 1918.
********** 1933 'Diversions and Pastimes' by R M Abraham, which was first published by Constable and Constable in London in 1933, gives nets for the Pyramid (Tetrahedron), Cube, Octahedron, Icosahedron, Dodecahedron, Rhombic Dodecahedron, Tetrahexahedron, Icositetrahedron, Triakisoctahedron, Cube and Octahedron, and Copper Sulphate crystal.
********** 1940 'El Plegado y Cartonaje en la Escuela Primaria' by Antonio M Luchia and Corina Luciani de Luchia, which was published by Editorial Kapelusz in Buenos Aires in 1940 contains a page showing standard polyhedral nets but also shows ways of constructing more complex nets, by paperfolding, which can be assembled without the need for glue.
********** |
|||||||