| The Public Paperfolding History Project
Last updated 28/1/2026 x |
|||||||
| Flexagons | |||||||
| This
page attempts to give a broad outline of what is known
about the origin and history of the flexible paper
novelties known as Flexagons. This is the overview page.
There are links within this page to further information
about the origin and history of some of the
sub-categories of flexagons such as hexaflexagons,
tetraflexagons, silverflexagons, bronzeflexagons and some
individual flexagons which deserve specail attention.
Please contact me if you know any of this information is
incorrect, if you have any other information that should
be added or are able to supply a copy of any of the
articles referred to which I have not seen. Thank you. It is worth noting that my interest in and knowledge of flexagons mostly relates to their use as entertainments, magic effects, puzzles and as a form of recreational paperfolding. While I have included references to mathematical articles, particularly on the hexaflexagons page, I am not a competent mathematician and have not attempted a history of the mathematical understanding of flexagons. Many of the less well known references on these pages have been borrowed from Peter Messer's Bibliography of Flexagons. Links to the history of the Chinese Wallet and Jacob's Ladder are included on this page. The Chinese Wallet is an early form of tetraflexagon. ********** The Chinese Wallet - 1502 onwards
********** Jacob's Ladder - 1820 onwards
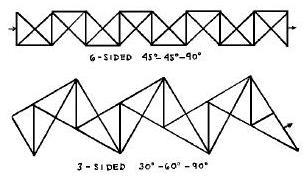
********** Possible existence of the Trick Book in the 1930s According to Martin Gardner's chapter about Tetraflexagons in 'The Second Scientific American Book of Mathematical Puzzles and Diversions', which was first published by Simon and Schuster in New York in 1961, the tetra-tetraflexagon 'has often been used as an advertising novelty because the difficulty of finding its fourth face makes it a pleasant puzzle. I have seen many such folders, some dating back to the 1930s. One had a penny glued to the hidden face'. This information is not included in the original article on which this chapter was based (published in 'Scientific American' in 1958). ********* Fall 1939 - The Discovery of Hexaflexagons According to an article titled 'Flexagons', written by Martin Gardner, which was published in issue 195 of Scientific American in Dec 1956, Arthur Stone discovered hexaflexagons, specifically the trihexaflexagon and hexahexaflexagon, when playing with inch wide strips of paper. With the help of friends Bryant Tuckerman, Richard Feynman and John Tukey (who together with Stone formed the 'Flexagon Committee') many other hexaflexagons were quickly discovered and analysed:
It seems clear that the word 'flexagon' in this article refers only to hexaflexagons not to other varieties. In 'A Conversation with Martin Gardner', a record of an interview conducted by Anthony Barcellos, which was published in The Two-Year College Mathematics Journal of Sept 1979, Vol. 10, No. 4, pp. 233-244, Martin Gardner gives the source of his information for this article as John Tukey and Bryant Tuckerman. 'I had sold them one previous article on logic machines, so I queried them about this second piece, explained what a flexagon was, and they said, "Go ahead." So I made a trip to Princeton and interviewed John Tukey and Bryant Tuckerman.' There is a separate page for further information about the history of hexaflexagons. ********** 1939 / 1940 - The study of tetraflexagons In his follow up article 'About Tetraflexagons and Tetraflexigation', which was published in the May 1958 issue of 'Scientific American', Martin Gardner indicates that a number of tetraflexagons were also discovered at this time. He says, 'Stone and his friends (notably John W Tukey, now a well-known topologist) spent considerable time folding and analysing these four-sided forms, but did not succeed in developing a comprehensive theory that would cover all their discordant variations. There is a separate page for further information about the history of tetraflexagons. ******** 1946 - Cherchez la Femme According to an article titled 'About Tetraflexagons and Tetraflexigation' by Martin Gardner, which was published in the May 1958 issue of 'Scientific American', the tetra-tetraflexagon novelty called Cherchez la Femme was 'copyrighted' in 1946.
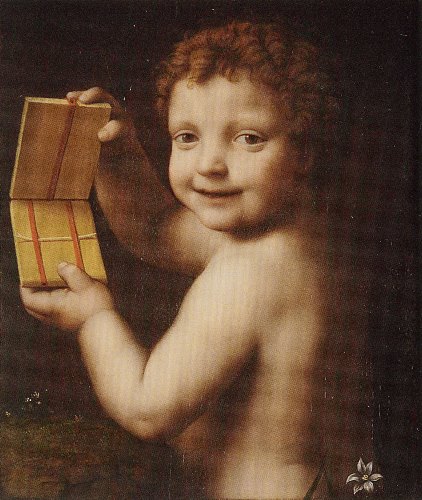
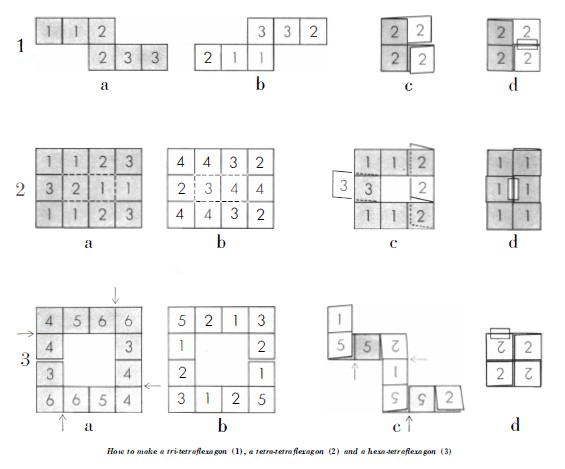
(Picture of one face of Cherchez la Femme courtesy of the Lilly Library, Indiana University, Bloomington, Indiana from the Jerry Slocum Mechanical Puzzle Collection.) There is a separate page for more information about Cherchez la Femme / The Trick Book ********** 1956 An article titled 'Flexagons', written by Martin Gardner, was published in issue 195 of Scientific American in Dec 1956. This article explained how to make and flex some basic straight strip hexaflexagons. It also stated that hexaflexagons had been invented in 1939 by Arthur Stone, then studying at Princeton, which were further developed by a 'Flexagon Committee' consisting of Stone himself, Bryant Tuckerman, Richard Feynman and John Tukey (all of whom were to go on to become famous in other ways) and that 'A complete mathematical theory of flexigation was worked out in 1940 by Tukey and Feynman.' There is no mention in the article of any flexagons other than hexaflexagons. According to the article 'Flexagons part one' in 'Xtra Credit 4' by Karl Fulves, published in 2009, the inspiration for this Martin Gardner article arose when 'Royal V Heath showed him a large coloured cloth hexahexaflexagon. Gardner interviewed the inventors.' ********** 1958 The May 1958 issue of 'Scientific American' included an article by Martin Gardner titled 'About Tetraflexagons and Tetraflexigation' which explains how to make and flex the tri-tetraflexagon, a tetra-tetraflexagon and a hexa-tetraflexagon. The article refers to both the Jacob's Ladder and the 'magic billfold' (presumably the Chinese Wallet) and 'Cherchez la Femme'. See various entries above. No 2, the tetra-tetra-flexagon is the same flexagon that he had previously used as the basis of his puzzle Cherchez la Femme.
*** This article also discusses the Flexatube. In introducing this puzzle Martin Gardner:
This does not sound to me like a description of the Flexatube but rather of the flexagon I call the Woven Flexatube, which, as the description says, can be flexed into a tube which can then be turned inside out by further flexing. I have published this as the puzzle Night and Day, but it may be that my puzzle is simply a reconstruction of something invented by Arthur Stone. In which case we must presume that Martin Gardner has confused the two designs and that the Flexatube was in fact invented by someone else entirely. A mystery ... Maybe sight of the letter referred to here would clear the mystery up. If this passage is a description of the Woven Flexatube then it is the first mention of a silverflexagon in the literature. There is a separate page for further information about the history of silverflexagons. There is also a separate page about the Flexatube puzzle. ********** 1960 A 'Hexa-hexa-flexagon Puzzle' appears in 'Paper Folding Fun' by Robert Harbin, which was published by Oldbourne in London in 1960.
********** 1962 There are two extant versions of an article about flexagons published in 1962 by RIAS (the Research Institute for Advanced Studies in Baltimore). One, held on the site of Erik Demaine, FLEXAGONS (erikdemaine.org), is titled Flexagons, referenced TR 62-11, dated May 1962 and attributed to Antony S Conrad and Daniel K Hartline. The other, held on the site of Harold V McIntosh, tflexagon.pdf (cinvestav.mx), is titled 'The Theory of the Flexagon' and said to be 'A faithful reproduction of a RIAS Miscellaneous Publication of the same title, apparently later numbered RIAS Technical Report 60-24'. This report is attributed to Conrad alone. Both reports are mainly a discussion of hexaflexagons but in the second there is also a chapter on other flexagons which illustrates strips for a silverflexagon and a bronzeflexagon.
As far as I know this is the first mention of a bronzeflexagon in the literature.There is a separate page for further information about the history of bronzeflexagons. The first report contains the sentence 'We may safely conjeture (sic) that such a simple object as the first flexagon must have been discovered long ago, and perhaps many times since. For example, there are reports of such a device existing in elementary schools in pre-war Vienna.' Unfortunately, no reference for this information is given. ********** 1971 'The Combinatorial Richness of Folding a Piece of Paper' by Martin Gardner, an article published in 'Scientific American' of May 1971, contained instructions for making a paperfolding puzzle by Henry Ernest Dudeney and three others by Robert E Neale, two of which are flexagons, the Cross Flexagon and the Sheep and Goats puzzle. The solutions were published in the June 1971 issue. The Cross Flexagon is a non-twisted tetraflexagon, as far as I know the first to be mentioned in the literature. The Sheep and Goats puzzle is a treatment of the Woven Flexatube silverflexagon, as far as I know the first puzzle based on a flexagon to be published. ********** 1976 Peter Messer provides a reference to a chapter titled 'Flexagons for the Magician' in 'Paper Folding Geometry' by D A Johnson, published by J Weson Walch, 1976. I have not been able to access a copy of this book and so do not know what it contains at present. ********** 2002 'The Annals of Statistics' Vol. 30, No. 6 of Dec., 2002, contains an article entitled 'John W. Tukey: His Life and Professional Contributions', by David R. Brillinger, pp. 1535-1575, which includes the following information.
********** 2003 'Flexagons Inside Out' by Les Pook, published by Cambridge University Press in 2003, contains a detailed analysis of and nets for many of the hexaflexagon and tetraflexagon families and an introduction to several other less well known types of flexagon such as convex polygon flexagons and star flexagons. Also contains a brief chapter on the early history of flexagons. ********** 2004 'Mathematics Magazine' Vol. 77, No. 5 of Dec., 2004 contained an article titled 'It's Okay to Be Square If You're a Flexagon' by Ethan J. Berkove and Jeffrey P. Dumont, pp. 335-348, which discusses some simple hexaflexagons and tetraflexagons. ********** 2009 'Serious Fun with Flexagons' by Les Pook, published by Springer in 2009 Concentrates on edge ring flexagons made from polygons of various shapes from a solid mechanics linkage perspective and shows how silver flexagons and bronze flexagons relate to these designs. ********** 2010 'The European Journal of Combinatorics' Volume 31, issue 1, of January 2010, contains an article titled 'The combinatorics of all regular flexagons' by Thomas Anderson, Bruce McLean, Homeira Pajoohesh and Chasen Smith, Pages 72-80. ********** 2012 'The College Mathematics Journal' Vol. 43, No. 1 of January 2012) contains an article 'From Hexaflexagons to Edge Flexagons to Point Flexagons' by Les Pook, pp. 11-14 ********** |
|||||||