Main Index Page

Last updated 19/2/2024

x

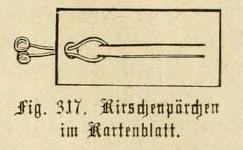
The puzzles on this page can all be solved through trial and error manipulation (although knowledge of a little simple mathenatics may help at times). There is a separate page for Mathematical Paperfolding Puzzles ie those puzzles which can only be solved using mathematics.

**********

The Cherries Puzzle - 1502 onwards

**********

1860

A puzzle solved by folding two latin numerals in half, just headed 'Autre subtilitie' (Another subtlety) but which I call 'Halving 9 and 13', appears in 'L'Ancienne et la Nouvelle Collection des Tours de Magie' by M Lecomte, which was published by S Borneman in Paris in 1860.

Roughly translated this reads, 'By betting that half of 9 is 4 and half of 13 is 8 you are necessarily putting a good number of betters against you, but you win easily by proving it in the following way ... All the finesse consists in writing the numbers as above and folding them along the dotted line.'

**********

1899

'L'illustre national' of 24th December 1899 contained a puzzle to be solved by folding a rectangle to find the image of a Russian. This puzzle was also published in other periodicals at a similar time.

**********

This is the solution, which was published in the issue for 18th February 1900.

**********

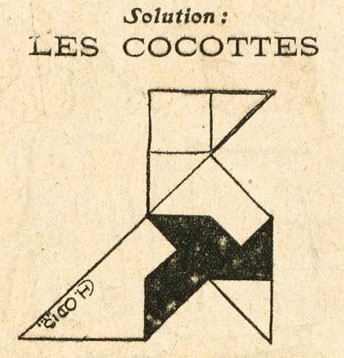
1901

Issue 166 of the Buenos Aires edition of 'Caras y Caretas' for 7th December 1901 included a puzzle to cut a rectangle into pieces that when rearranged would form a Cocotte / Pajarita.

**********

The solution was published in the following issue, no 167 of 14th December 1901.

**********

1908

The 'Supplément illustré' of the issue of 'Mémorial d'Amiens et du département de la Somme', for 12th July 1908 contained a puzzle to be solved by folding a decorated square. It is likely that it was also published in other periodicals at a similar time.

**********

The solution was published in the issue for 30th August 1908.

**********

1910

This puzzle was published in the issue of 'Mémorial d'Amiens et du département de la Somme', for 2nd October 1910.

**********

The solution was published in the issue for 25th December 1910.

**********

This puzzle was published in the issue of 'Mémorial d'Amiens et du département de la Somme', for 20th November 1910.

**********

The solution was published in the issue for 5th March 1911.

**********

This surprisingly similar puzzle was published in the issue of 'Mémorial d'Amiens et du département de la Somme' for 25th December 1910.

**********

The solution was published in the issue for 19th March 1911.

**********

1911

This puzzle was published in the issue of 'Mémorial d'Amiens et du département de la Somme', for 22nd January 1911.

**********

The solution was published in the issue for 2nd April 1911.

**********

Pattern Drawing Puzzles Solved by Folding Paper - 1918 onwards

**********

The Stamp Folding Puzzle - 1931 onwards

**********

The Flexatube - c1939 onwards

**********

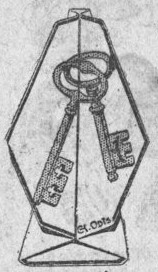
c1942 - Lock 'em Up

**********

Robert Neale's Beelzebub - 1971 onwards

This puzzle by Robert Neale was first published in Martin Gardner's article 'The combinatorial richness of folding a piece of paper' which appeared in 'Scientific American' Vol. 224, No. 5 of May 1971, pp. 110-117. The solution was published the following month.

**********

Robert Neale's Sheep and Goats - 1971 onwards

This puzzle by Robert Neale was first published in Martin Gardner's article 'The combinatorial richness of folding a piece of paper' which appeared in 'Scientific American' Vol. 224, No. 5 of May 1971, pp. 110-117. The puzzle is a treatment of the Woven Flexatube. The object is to transform the flexagon to separate the white and black areas so that, when solved, one face of the flexagon is all white and the other all black. The solution was published the following month.

**********