| Origami Heaven A paperfolding
paradise
The website of
writer and paperfolding designer David Mitchell
x
|
| |
| Modular
Polyhedra - Flat-Faced Designs |
| |
| There is a separate page for
Flat faced Cubes and Silverhedra |
| |
| Deltahedra |
| |
| I use the term deltahedra to
refer to solids whose faces are all equilateral
triangles. |
| |
| Regular
Tetrahedra |
| |
 |
|
Name: Mirror-Image
Tetrahedron Modules / Paper
shape / Folding geometry: 2 mirror-image modules
from double bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 1996.
Reference:
131
Diagrams:
Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X // In Portuguese - Origami
matematicos - Republicao - ISBN 972-570-257-3
|
|
| |
 |
|
Name: Robust Mirror-Image
Tetrahedron Modules / Paper
shape / Folding geometry: 2 mirror-image
equilateral modules from bronze rectangles using
60/30 degree folding geometry.
Designer /
Date: David Mitchell, 1998
Reference:
162
Diagrams:
Not yet available.
|
|
| |
 |
|
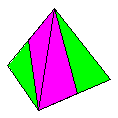
Name: Variable Tetrahedra.
The positions of the flaps and pockets can be
varied to create five tetrahedra, all of
identical appearance, but each made from a
different combination of modules. Modules / Paper
shape / Folding geometry: 2 modules from bronze
rectangles using 60/30 degree folding geometry.
Designer /
Date: David Mitchell, 2017
Reference:
575
Diagrams:
As Regular Tetrahedra in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
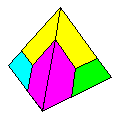
Name: Striped Mirror-Image
Tetrahedron Modules / Paper
shape / Folding geometry: 2 mirror-image Abe or
Terada modules or the equivalent geometry
embedded in squares. 60/30 degree folding
geometry.
Designer /
Date: David Mitchell, 2003.
Reference:
534
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Quartetra
- four part modular assembly puzzle. Paper type / shape:
Hexagon / Any kind of paper.
Designer /
Date: David Mitchell, 1988.
Reference:
030
Diagrams:
Paperfolding Puzzles - Water Trade - ISBN
0-9534774-0-X // Paperfolding Puzzles (2nd Edition) -
David Mitchell - Water Trade - ISBN
978-0-9534774-5-6
|
|
| |
 |
|
Name: Reptile
Tetrahedron Modules / Paper
shape / Folding geometry: 12 Reptile modules from
squares using 60/30 degree folding geometry.
Designer /
Date: David Mitchell, 1997.
Reference:
146
Diagrams:
BOM 189 April 1998 // On-line diagrams are
available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: 12-part Tetrahedron Modules / Paper
shape / Folding geometry: 12 modules from silver
rectangles using 60/30 degree folding geometry.
Designer /
Date: David Mitchell,1991.
Reference:
081
Diagrams:
In BOS Convention Pack Spring 1992.
|
|
| |
| Equilateral
Hexahedra |
| |
.gif) |
|
Name: Robust
Diamond Hexahedron Modules / Paper
shape / Folding geometry: 6 equilateral modules
in 2 sets of 3 mirror-image versions folded from
bronze rectangles using 60/30 degree folding
geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
162
Diagrams:
As Diamond Hexahedron in Mathematical Origami - David Mitchell -
Tarquin publications - ISBN 9781911093169
|
|
| |
| Regular
Octahedra and other Deltahedral Bi-Pyramids |
| |
 |
|
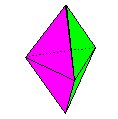
Name: Robust
Triangular Equilateral Bi-Pyramid Modules / Paper
shape / Folding geometry: 3 equilateral modules
folded from bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
162
Diagrams:
As Triangular Equilateral Bi-Pyramid in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
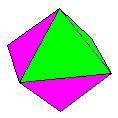
Name: Regular
Octahedron (2-part). Not robust. Modules / Paper
shape / Folding geometry: 2 modules folded from
double bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 1997.
Reference:
144
Diagrams:
Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X // In Portuguese - Origami
matematicos - Republicao - ISBN 972-570-257-3
|
|
| |
 |
|
Name: Robust
Octahedron Modules / Paper
shape / Folding geometry: 4 equilateral modules
folded from bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 1998.
Reference:
162
Diagrams:
As Regular Octahedron in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
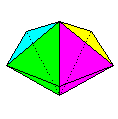
Name: Robust
Pentagonal Equilateral Bi-Pyramid Modules / Paper
shape / Folding geometry: 5 equilateral modules
folded from bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
162
Diagrams:
As Pentagonal Equilateral Bi-Pyramid in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
| Regular
Icosahedra |
| |
 |
|
Name: Robust
Icosahedron Modules / Paper
shape / Folding geometry: 10 equilateral modules
in 2 sets of 5 mirror-image versions folded from
bronze rectangles using 60 degree folding
geometry.
Designer /
Date: David Mitchell, 1998.
Reference:
162
Diagrams:
As Regular Icosahedron in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
Name: Striped
Mirror-Image Icosahedron - can be made
from Abe or Terada modules or from the equivalent
designs embedded in squares. Modules / Paper
shape / Folding geometry: 10 modules in 2 sets of
5 mirror-image versions folded from bronze
rectangles or squares using 60/30 degree folding
geometry.
Designer /
Date: Modules - Various. Assembly - David
Mitchell, 2003.
Reference:
Diagrams:
Not yet available.
|
|
| |
| The
Equilateral Dodecahedron |
| |
 |
|
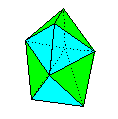
Name: The
Robust Equilateral Dodecahedron Modules / Paper
shape / Folding geometry: 6 equilateral modules
in 2 sets of 3 mirror-image versions folded from
bronze rectangles using 60 degree folding
geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
162
Diagrams:
As the Equilateral Dodecahedron in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
| The
Equilateral Hexakaidecahedron |
| |
 |
|
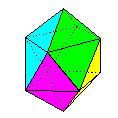
Name: The
Robust Equilateral Hexacaidecahedron Modules / Paper
shape / Folding geometry: 8 equilateral modules
in 2 sets of 4 mirror-image versions folded from
bronze rectangles using 60 degree folding
geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
162
Diagrams:
As Equilateral Hexacaidecahedron in Mathematical Origami - David Mitchell -
Tarquin publications - ISBN 9781911093169
|
|
| |
| The
Equilateral Heccaidecahedron |
| |
| Details not yet available. |
| |
| Regular
Dodecahedra |
| |
 |
|
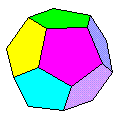
Name: Regular
Dodecahedron - full-face module version
- not robust. Modules / Paper shape / Folding
geometry: 12 modules from squares using mock
platinum folding geometry.
Designer /
Date: David Mitchell, 1996.
Reference:
126
Diagrams:
Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X // In Portuguese - Origami
matematicos - Republicao - ISBN 972-570-257-3
|
|
| |
 |
|
Name: Robust
Dodecahedron. Versions only differ in
paper shape used. Version 1: Faces
stand slightly proud.
Modules /
Paper shape / Folding geometry: 30 modules from
silver rectangles.
Designer /
Date: David Mitchell, 1992. Possibly invented at
an earlier date by David Brill.
Reference:
576
Diagrams:
Not published.
Version
2: Flat faces.
Modules /
Paper shape / Folding geometry: 30 modules from
mock platinum rectangles.
Designer /
Date: David Mitchell, 2016.
Reference:
576
Diagrams:
As Regular Dodecahedron in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
| Rhombic
and Semi-Rhombic Polyhedra |
| |
| When I
was writing the first edition of my book, Mathematical
Origami, I found that I wanted to include several
polyhedra for which there did not appear to be an
established mathematical name. The characteristics of
these polyhedra were that their faces were either
109.28/70.32 rhombuses or 70.32/54.84/54.84
(1:sqrt3/2:sqrt3/2) triangles, which can be obtained by
folding the 109.28/70.32 rhombus in half lengthways, or a
mixture of the two. For want of better, I stole the word
'rhombic' from the name of the rhombic dodecahedron,
whose faces are, of course, 109.28/70.32 rhombuses, and
applied it to the other polyhedra as well, thus creating
the terms rhombic tetrahedron, rhombic octahedron etc and
the general term rhombic polyhedra to describe them as a
group. I justified this usage to myself on the grounds
that the triangular faces occurred in pairs, which if
flattened would come back to a 109.28/70.32 rhombus.
Somewhat to my surprise, my publisher raised no objection
to this.
I was expecting
that I would receive a barrage of criticism for this
usage and that someone would soon point out to me a
better terminology to use for these forms, but, so far,
neither of these things have happened. I still, however,
expect a better terminology to emerge at some stage.
Pro tem then I
shall continue to use the term rhombic polyhedra,
although in a slightly developed sense, to mean the set
of those polyhedra which can be combined with other
identical polyhedra to build a rhombic dodecahedron and
which have at least some faces that are either
109.28/70.32 rhombuses or 70.32/54.84/54.84
(1:sqrt3/2:sqrt3/2) triangles. The members of this
interesting set of polyhedra are illustrated below. All
of them will fill space.
This definition
deliberately excludes many polyhedra whose faces are
70.32/54.84/54.84 (1:sqrt3/2:sqrt3/2) triangles, and
particularly those that can be made by putting together
three-sided pyramids, or sunken pyramids, whose faces are
such triangles and similar designs whose faces are or
include 109.28/35.36/35.36 (sqrt2:sqrt3/2:sqrt3/2)
triangles, which can be obtained from the 109.28/70.32
rhombus by folding it in half in the other direction. If
these forms were to be included within the definition of
rhombic polyhedra then we would be in a situation where
there were, for instance, three separate forms that could
quite correctly be called rhombic hexahedra and three
more that could quite correctly be called rhombic
dodecahedra. This is clearly nonsensical and so I have
adopted the narrower definition given above. I have not
invented any general name for the excluded forms.
It is worth
pointing out that although the 109.28/70.32 rhombus has
diagonals in the proportion 1:sqrt2 I have avoided using
the term silver rhombus since that would suggest that
this rhombus has properties similar to the silver
rectangle and silver triangle, which it does not.
The classic book
Mathematical Models, by H M Cundy and A P Rollett
contains a net for the rhombic pyramid, although the
authors do not give it a name. They do, however, use the
term rhombic polyhedra in a different sense from mine as
a general term for polyhedra whose faces are rhombuses,
ie the cube, the rhombic dodecahedron and the
triacontahedron. I apologise for introducing confusion by
using this term in another way.
The third edition
of this book, published in 1960, also contains the
information that a Mr Dorman Luke, otherwise unknown to
me, has found that all three stellations of the rhombic
dodecahedron can be arrived at by adding what I call
rhombic pyramids to the rhombic dodecahedron in
successively larger numbers. These forms fall outside my
definition of rhombic polyhedra but this is not a
difficulty as they already have their own established
names. I have, incidentally, found that by continuing the
process of adding rhombic pyramids to the third
stellation it is eventually possible to arrive at a much
larger rhombic dodecahedron than the one used to initiate
the process.
|
| |
| Rhombic
and Semi-Rhombic Tetrahedra |
| |
 |
|
Name: The Mirror-Image
Rhombic Tetrahedron. Modules / Paper
shape / Folding geometry: 2 mirror-image modules
folded from silver rectangles.
Designer /
Date: David Mitchell, 1996.
Reference:
129
Diagrams:
Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X // In Portuguese - Origami
matematicos - Republicao - ISBN 972-570-257-3
|
|
| |
 |
|
Name: The Robust
Mirror-Image Rhombic Tetrahedron. Modules / Paper
shape / Folding geometry: 2 mirror-image
truncated Robinson modules folded from silver
rectangles.Three versions possible as the set of
modules can be configured and assembled in three
different ways.
Designer /
Date: David Mitchell, 1998.
Reference:129
Diagrams:
Diagrams not yet available.
|
|
| |
 |
|
Name: The Variable Rhombic
Tetrahedron Modules / Paper
shape / Folding geometry: 2 modules from double
silver rectangle strip. Three versions possible
as the set of modules can be configured and
assembled in three different ways.
Designer /
Date: David Mitchell, 2017
Reference:
545
Diagrams:
Diagrams not yet available.
|
|
| |
 |
|
Name: Pocket Rhombic
Tetrahedron Modules / Paper
shape / Folding geometry: 2 modules from 1x3/4
silver rectangles using silver rectangle
geometry.
Designer /
Date: David Mitchell, 1994.
Reference:
113
Diagrams:
Diagrams not yet available.
|
|
| |
 |
|
Name: The Variable Rhombic
Tetrahedron. The positions of the flaps
and pockets can be varied to create five
tetrahedra, all of identical appearance, but each
made from a different combination of modules. Modules / Paper
shape / Folding geometry: 2 mirror-image modules
folded from silver rectangles.
Designer /
Date: David Mitchell, 2017.
Reference:
Diagrams:
As the Rhombic Petrahedron in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169.
|
|
| |
 |
|
Name: The Semi- Rhombic
Tetrahedron Modules / Paper
shape / Folding geometry: 2 modules folded from
silver rectangles.
Designer /
Date: David Mitchell, 2017.
Reference:
547
Diagrams:
In Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
| Rhombic
Hexahedra |
| |
 |
|
Name: The Rhombic Hexahedron
- replihedron which is one third of a
rhombic dodecahedron. Modules / Paper
shape / Folding geometry: 2 modules folded from
silver rectangles.
Designer /
Date: David Mitchell, 2004.
Reference:
268
Diagrams:
Diagrams not yet available.
|
|
| |
| |
| |
| Rhombic
Octahedra |
| |
 |
|
Name: The Assymetric Rhombic
Octahedron Modules / Paper
shape / Folding geometry: 2 modules folded from
silver rectangles.
Designer /
Date: David Mitchell, 2004.
Reference:
266
Diagrams:
Diagrams not yet available.
|
|
| |
| |
| |
| The
Rhombic Pyramid, the Semi-Rhombic Pyramid and the Square
Base Rhombic Pyramid |
| |
 |
|
Name: The
2-part Rhombic Pyramid Modules / Paper
shape / Folding geometry: Made by combining a
rhombic four-pockets module with a rhombic hat /
Both folded from silver rectangles.
Designer /
Date: David Mitchell, 2000.
Reference:
147
Diagrams:
In Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
Name: The Square
Base Rhombic Pyramid Modules / Paper
shape / Folding geometry: 4 modules from silver
rectangles.
Designer /
Date: David Mitchell, 2017.
Reference:
543
Diagrams:
In Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
| Rhombic
Dodecahedra |
| |
 |
|
Name: Kite
Pattern Rhombic Dodecahedron Modules / Paper
shape / Folding geometry: 24 modules from silver
rectangles.
Designer /
Date: David Mitchell, 1990.
Reference:
067
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: David
Mitchell's Rhombic Dodecahedron (so
named to distinguish it from Nick Robinson's
Rhombic Dodecahedron, from which it is derived). Modules / Paper
shape / Folding geometry: 12 rhombic triangle
modules folded from silver rectangles.
Designer /
Date: David Mitchell, 2004.
Reference:
267
Diagrams:
In Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
| The
First Stellated Rhombic Dodecahedron |
| |
 |
|
Name: 6-part
Stellated Rhombic Dodecahedron Modules / Paper
shape / Folding geometry: 6 modules from silver
rectangles using silver rectange folding
geometry.
Designer /
Date: David Mitchell, 1989.
Reference:
042
Diagrams:
Reviewed in BOM 139 December 1989 // Wonderful
World of Modulars - Tomoko Fuse - 4-405-07553-0 -
published in Japanese // BOS Convention Pack
Autumn 1989 - diagrams drawn by Francis Ow //
Photo on Gallery section of Origami: The Complete
Guide to the Art of Paperfolding - Rick Beech -
Lorenz Books (Anness Publishing) - ISBN 075480782
// Photo on cover of Russian Origami Society
magazine issue 3 1999 // Orison 6 2009 // Also in
Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169 // On-line diagrams are available
on the Modular Designs page of this site.
|
|
| |
 |
|
Name: 24-part
Stellated Rhombic Dodecahedron - made by
adding 'hats' to Nick Robinson's Rhombic
Dodecahedron. Modules / Paper shape / Folding
geometry: 24 modules in two sets of twelve from
silver rectangles using silver rectangle folding
geometry.
Designer /
Date: David Mitchell, 1997.
Reference:
150
Diagrams:
Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X // In Portuguese - Origami
matematicos - Republicao - ISBN 972-570-257-3 //
Quadrato Magico 101 Autumn 2011
|
|
| |
| Other
Flat-Faced Polyhedra |
| |
.gif) |
|
Name: The
Robust Diamond Hexahedron Modules / Paper
shape / Folding geometry: 6 equilateral modules
in 2 sets of 3 mirror-image versions folded from
bronze rectangles using 60 degree folding
geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
Diagrams:
As the Diamond Hexahedron in Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
Name: The
Square Base Equilateral Pyramid Modules / Paper
shape / Folding geometry: 4 modules from
silverdouble bronze rectangles using 60 degree
folding geometry.
Designer /
Date: David Mitchell, 2017.
Reference:
Diagrams: Mathematical Origami (2nd Edition) -
David Mitchell - Tarquin publications - ISBN
9781911093169
|
|
| |
 |
|
Name: Compound of Cube and
Octahedron - made by adding hats to the
Twisted Square Cube. 12 squares. Modules / Paper
shape / Folding geometry: 6 modules from squares
using standard folding geometry and 6 from
squares using 60/30 degree folding geometry..
Designer /
Date: David Mitchell, 2016.
Reference:
541
Diagrams:
Not yet available.
|
|
| |
 |
|
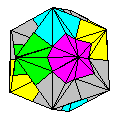
Name: Great
Dodecahedron Modules / Paper
shape / Folding geometry: 12 modules from
pentagons.
Designer /
Date: David Mitchell, 1990.
Reference:
061
Diagrams:
Diagrams not yet available.
|
|
| |
 |
|
Name: Small
Stellated Dodecahedron (30-part) Modules / Paper
shape / Folding geometry: 30 modules from squares
using mock platinum folding geometry.
Designer /
Date: David Mitchell, 1990.
Reference:
536
Diagrams:
Diagrams not yet available.
|
|
| |
 |
|
Name: Small
Stellated Dodecahedron (60-part) -
Design from squares that allows each of the
pentagrams visible on the surface of the form to
be made from paper of a different colour. Modules / Paper
shape / Folding geometry: 60 modules from squares
using mock platinum folding geometry.
Designer /
Date: David Mitchell, 2016.
Reference:
537
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Spiky
Star Modules / Paper shape / Folding
geometry: 30 modules from 2x1 rectangles using
standard rectangle folding geometry.
Designer /
Date: David Mitchell, 2001.
Reference:
238
Diagrams:
Diagrams not yet available.
|
|
| |
 |
|
Name: Kite
Pattern Triacontahedron Modules / Paper
shape / Folding geometry: 60 modules from custom
rectangles using golden rectangle folding
geometry.
Designer /
Date: David Mitchell, 1990.
Reference:
068
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
| |





.gif)



























