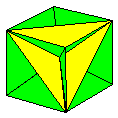
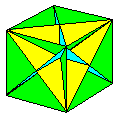
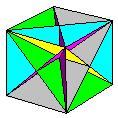
The first edition of Mathematical Origami was published in 1997 and had 64 pages. The much more substantial second edition, published in 2020, has 144. Only six of the designs in the first edition survive in the second. The main contents of the second edition are illustrated below. Except where otherwise stated all the designs in the book are my own.

Like the first, the second edition is primarily aimed at mathematics teachers, although I hope that recreational mathematicians and modular origami aficionados will also find much in it to enjoy and enthuse about. The bulk of the book explains how to fold simple units, the modules, from ordinary photocopy paper and how to assemble them, usually without the need for glue, into polyhedra which are sufficiently robust to stand up to reasonably rough handling in a classroom setting.

The advantages of making polyhedra in this way are:

• The process of creating the necessary starting shapes and of folding the modules is itself highly mathematical in nature

• Modules / polyhedra can be made as group projects

• All polyhedra built from the same type of module will have faces to scale and can therefore be used as the basis for combination puzzles and to demonstrate that they will fill (or not fill) space

• Finished polyhedra can be taken apart and the modules re-used to build other polyhedra of the same class

• Modules of different colours can be swapped around within the same polyhedral form to create different surface colourings

• Damaged modules can easily be replaced

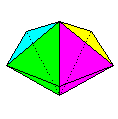
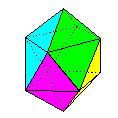
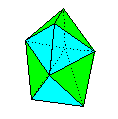
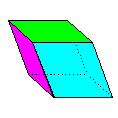
The book is divided into three main sections: Equilateral Deltahedra, Rhombic and Semi-Rhombic Polyhedra and Planar Polyhedra, with a few outliers, the Cube, the Regular Dodecahedron and the Triancontahedron. Of these the Rhombic and Semi-Rhombic Polyhedra should be of particular interest as many of them, so far as I am aware, are not treated of elsewhere.

The modules are folded from a range of rectangles of differing proportions, squares, silver rectangles, bronze rectangles, mock platinum rectanglesn and golden rectangles. Using a range of rectangles makes folding the modules much easier than is sometimes the case with other systems of modular polyhedral design. The book also shows you how to fold templates to make it easy to construct rectangles of the correct proportions in the quantities required.

The second edition of Mathematical Origami can be purchased in hardcover, paperback or various ebook formats from: https://www.tarquingroup.com/mathematical-origami-second-edition.html. In case of difficulty you can contact the sales team via the web-based contact form at https://www.tarquingroup.com/contacts/

Unfortunately the designer of the cover randomly decided to include a picture of a modular paper sculpture (the blue image) which has nothing whatsoever to do with the contents or ethos of the book. This design is called Taygeta and is by Alexander Frolov. The information on the front and back covers regarding the sections into which the book is divided is also incorrect. It relates to an early draft rather than the finished book.