| Origami Heaven A paperfolding paradise The website of writer and paperfolding designer David Mitchell x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
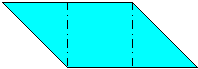
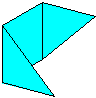
Parallelogram modules are, somewhat unsurprisingly, a family of modules whose basic outline is that of a parallelogram, although the acute points of this parallelogram may be truncated. These modules have two pockets and two tabs which are arranged alternately around the module, tab, pocket, tab, pocket. The tabs are triangular and the central area between the tabs, that contains the pockets, is a square or a rhombus. The shape of the central area and, of course, of the parallelogram as a whole, is determined by the folding geometry of the module. Parallelogram modules always have right handed and left handed mirror-image forms. Many of the best known and most elegant modules are parallelogram modules, including:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Modules folded using standard folding geometry | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
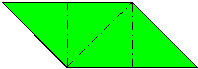
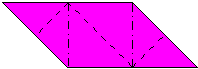
| As far
as I know all parallelogram modules folded using standard
folding geometry are the same basic shape and can be
configured in the same way. The simplest way to configure
this type of module, to make either a 6-part or 24-part
cube, is to make either one fold (for the 24-part Cube)
or two folds (for the 6-part cube) along the boundary
(ies) between the central square area of the module and
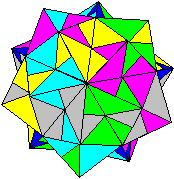
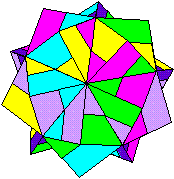
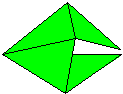
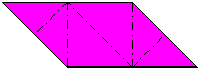
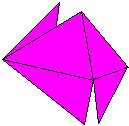
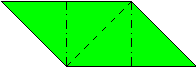
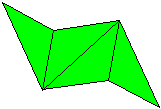
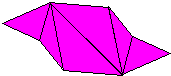
its tabs. It is also possible to configure parallelogram modules by making diagonal folds in either direction across the central square area (with ancillary configuring folds as required). One of these possibilities was discovered early on by Mitsonobu Sonobe who used it to create a 12-part cube. Toshie Takahama reversed the direction of this fold to create the module for her Jewel (which is technically a 3-part silverhexahedron). The modules (sometimes known as 'limping seagulls') that are used to make Stubby Stars are also folded using this diagonal crease. I call modules that are configured using a diagonal crease in this direction alpha modules. The possibility of configuring parallelogram modules by making a diagonal fold across the central area in the alternative direction is still little known at the time of writing (December 2015). I call modules configured in this way beta modules. I first discovered beta modules in 1989 while playing around with silveroctahedral forms made from Letterbox modules but didn't realise the significance of what I had found until I revisited the designs in 2012. At that point I realised that beta modules were not only useful in making silveroctahedra but would also make all the same forms as alpha modules (although beta versions are not always as stable as alpha versions). In looking for antecedents I found that Tomoko Fuse published a 12-part beta Sonobe module cube in the 1980's. A basic beta Sonobe module can also be found in Origami for the Connoisseur by Kunihiko Kasahara and Toshie Takahama, which was first published in Japanese in 1985 and in English in 1987. The idea does not appear, however, to have been developed significantly further in either case. The difference in the way the modules are configured necessarily alters the way the surface of the form is divided amongst the modules (the modular method) and this in turn may affect the pattern visible on the surface of the form (the modular pattern). The effect of folding 20-part 30-point Stubby Stars from alpha and beta Letterbox modules can be seen here: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| It is
also possible to create compound parallelogram modules. Parallelogram modules folded using standard folding geometry can be used to make cubes, cube combinations (cubes that are joined together at the edges or the corners) and silverhedra (polyhedra whose faces are 1:1:sqrt2 or silver triangles). Silverhedra can be created from deltahedra (polyhedra whose faces are equilateral triangles) by either pimpling or dimpling the faces (or by pimpling some faces and dimpling others). I call deltahedra with pimpled faces Stubby Stars for obvious reasons. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
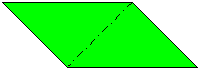
| Configuration patterns for parallelogram modules from standard folding geometry | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||