| The Public Paperfolding History Project
x |
|||||||
| Tetraflexagons | |||||||
| This
page attempts to give a broad outline of what is known
about the origin and history of Tetraflexagons. Please
contact me if you know any of this information is
incorrect, if you have any other information that should
be added or are able to supply a copy of any of the
articles referred to which I have not seen. Thank you. It is worth noting that my interest in and knowledge of flexagons mostly relates to their use as entertainments, magic effects, puzzles and as a form of recreational paperfolding. While I have included references to mathematical articles, I am not a competent mathematician and have not attempted a history of the mathematical understanding of flexagons. It is also worth noting that tetraflexagons are flexagons with rectangular, and not just square, faces. Links to the history of the Chinese Wallet and Jacob's Ladder are included on this page. The Chinese Wallet is an early form of tetraflexagon. ********** The Chinese Wallet - 1502 onwards
********** Jacob's Ladder - 1820 onwards
********** Possible existence of the Trick Book in the 1930s According to Martin Gardner's chapter about Tetraflexagons in 'The Second Scientific American Book of Mathematical Puzzles and Diversions', which was first published by Simon and Schuster in New York in 1961, the tetra-tetraflexagon 'has often been used as an advertising novelty because the difficulty of finding its fourth face makes it a pleasant puzzle. I have seen many such folders, some dating back to the 1930s. One had a penny glued to the hidden face'. This information is not included in the original article on which this chapter was based (published in 'Scientific American' in 1958). ********* 1939 According to an article titled 'About Tetraflexagons and Tetraflexigation', which was published in the May 1958 issue of 'Scientific American', Martin Gardner indicates, in 1939, 'Stone and his friends (notably John W Tukey, now a well-known topologist) spent considerable time folding and analysing these four-sided forms, but did not succeed in developing a comprehensive theory that would cover all their discordant variations. ******** 1946 According to an article titled 'About Tetraflexagons and Tetraflexigation' by Martin Gardner, which was published in the May 1958 issue of 'Scientific American', the tetra-tetraflexagon novelty called Cherchez la Femme was 'copyrighted' in 1946.
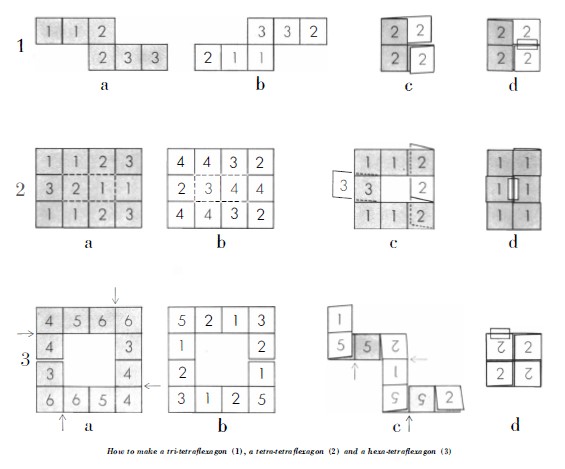
(Picture of one face of Cherchez la Femme courtesy of the Lilly Library, Indiana University, Bloomington, Indiana from the Jerry Slocum Mechanical Puzzle Collection.) There is a separate page for more information about Cherchez la Femme / The Trick Book ********** 1958 The May 1958 issue of 'Scientific American' included an article by Martin Gardner titled 'About Tetraflexagons and Tetraflexigation' which explains how to make and flex the tri-tetraflexagon, a tetra-tetraflexagon and a hexa-tetraflexagon. The article refers to both the Jacob's Ladder and the 'magic billfold' (presumably the Chinese Wallet) and 'Cherchez la Femme'. See various entries above. No 2, the tetra-tetra-flexagon is the same flexagon that he had previously used as the basis of his puzzle Cherchez la Femme.
********** 1961 'The Second Scientific American Book of Mathematical Puzzles and Diversions' by Martin Gardner, which was first published by Simon and Schuster in New York in 1961, contains a chapter titled 'Tetraflexagons'. I believe this contains fundamentally the same information that had been previously published in 'Scientific American' in 1958. ********** An article titled 'Square Flexagons' by P B Chapman was published in 'The Mathematical Gazette' 45:192-4, of October 1961. The article generalises the methodology applied to hexaflexagons in Wheeler 1958 to the development of tetraflexagons. ********** 1971 'The Combinatorial Richness of Folding a Piece of Paper' by Martin Gardner, an article published in 'Scientific American' of May 1971, contained instructions for making a paperfolding puzzle by William Dudeney and three others by Robert E Neale, two of which are flexagons, the Cross Flexagon (in its basic undecorated version) and the Sheep and Goats puzzle. The solutions were published in the June 1971 issue. As far as I know this is the first mention of a non-twisted tetraflexagon (the Cross Flexagon) in the literature. ********** 1976 Peter Messer provides a reference to a chapter titled 'Flexagons for the Magician' in 'Paper Folding Geometry' by D A Johnson, published by J Weson Walch, 1976. This book may contain information about tetraflexagons but I have not been able to access a copy to verify this. ********** 1978 'Flexagons' by Paul Jackson, published as Booklet No 11 of the British Origami Society in 1978, contains instructions for making and flexing the Window Flexagon (a non-twisted hexa-tetraflexagon made from a square ring of 12 squares) and Robert E Neale's non-twisted Cross Flexagon (a cross-shaped strip of 12 squares separated by a central slit, also in the form of a cross). ********** 1989 'Mathematical Curiosities 2' by Gerald Jenkins and Anne Wild, published by Tarquin in 1989, contains a net for a hexa-tetraflexagon. This is a republication of a book originally published in 1981. I have not been able to check if these designs were included in the original 1981 publication. ********** 1997 'Folding Money Fooling' by Robert E Neale, which was published by Kaufman and Company in 1997, explains how to construct and flex a tetraflexagon which the author calls 'Flexabill', because it is made from a dollar bill and developed from the cut and fold optcal illusion known as Hyperflex. This bi-directional tetraflexagon has four states which can be accessed in a complete cycle using two rolling and two tube flexes. ********** 1998 'The Magic of Flexagons' by David Mitchell, published by Tarquin publications in 1998, is a cut out and glue together book of flexagons and other flexible devices. It contains the Hidden Aces Flexagon (a non-twisted tetraflexagon with rectangular leaves, made from a 4x4 grid from which the corner and two central rectanges have been removed), the Double Cross Flexagon (aka the StaircaseTetraflexagon, a bi-directional twisted tetraflexagon with 7 states that can be changed from a right-handed version to a left-handed version and vice versa) and the Magic Square Flexagon (a tetraflexagon-like design which opens up to reveal a hidden Black Hole). ********** 1999 'The Mathemagician and Pied Puzzler, a collection in tribute to Martin Gardner', edited by Elwyn Berkelkamp and Tom Rodgers, was published by - A R Peters in 1999. It contains a chapter titled 'Self-Designing Tetraflexagons' by Robert E Neale which considers various ways in which non-twisted tetraflexagons can be constructed by removing areas from, or cutting slits into the centre of, a square. The designs explained are the Cross Flexagon, the Window Flexagon (two different folding methods), and several flexagons made from complete squares slit in various ways (which are not given names). The author notes that ' The first flexagon I saw that did not need glue (ie a non-twisted flexagon) was shown to me by Giuseppe Baggi years ago.' The context makes it clear that this is a reference to the Window Flexagon. This must have been in or prior to 1972 when Giuseppe Baggi died. The author also notes that the ms for this chapter was first submitted for publication in 1993 'but written more than a year or two before that.' ********** 2002 'Flexagons and Flexigation' by David Mitchell, privately published in 2002, provides a basic introduction to tetraflexagons and how to map them and includes some simple flexagon-based puzzles and magical effects. Explains the Tri-tetraflexagon, the Tri-Tetraflexagon Tube Challenge (finding a basic Black Hole), the 3-Row Tri-tetraflexagon , the Ribbon Release Trick and the Penetration Puzzle (finding a more sophisticated Black Hole), and the 3-state Linear Tetraflexagon. This publication can now be accessed online here. ********** 2003 'Flexagons Inside Out' by Les Pook, published by Cambridge University Press in 2003, contains a detailed analysis of and nets for many of the hexaflexagon and tetraflexagon families and an introduction to several other less well known types of flexagon such as convex polygon flexagons and star flexagons. Also contains a brief chapter on the early history of flexagons. ********** 2004 'Mathematics Magazine' Vol. 77, No. 5 of Dec., 2004 contained an article titled 'It's Okay to Be Square If You're a Flexagon' by Ethan J. Berkove and Jeffrey P. Dumont, pp. 335-348, which discusses some simple hexaflexagons and tetraflexagons. ********** |