Main Index Page

x

It is worth noting that my interest in and knowledge of flexagons mostly relates to their use as entertainments, magic effects, puzzles and as a form of recreational paperfolding. While I have included references to mathematical articles, I am not a competent mathematician and have not attempted a history of the mathematical understanding of flexagons.

**********

1958

The May 1958 issue of 'Scientific American' included an article by Martin Gardner titled 'About Tetraflexagons and Tetraflexigation' which explains how to make and flex the tri-tetraflexagon, a tetra-tetraflexagon and a hexa-tetraflexagon but also discusses the Flexatube puzzle. In introducing this puzzle Martin Gardner says:

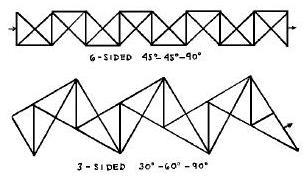
This does not sound to me like a description of the Flexatube, but rather of the silverflexagon I call the Woven Flexatube, which, as the description says, can be flexed into a tube which can then be turned inside out by further flexing. I have published this as the puzzle Night and Day, but it may be that my puzzle is simply a reconstruction of something invented by Arthur Stone. In which case we must presume that Martin Gardner has confused the two designs and that the Flexatube was in fact invented by someone else entirely. A mystery ... Maybe sight of the letter referred to here would clear the mystery up.

If this passage is a description of the Woven Flexatube then, as far as I know, it is the first mention of a silverflexagon in the literature.

**********

1961

'The Second Scientific American Book of Mathematical Puzzles and Diversions' by Martin Gardner, which was first published by Simon and Schuster in New York in 1961, contains a chapter titled 'Tetraflexagons'. I believe this contains fundamentally the same information that had been previously published in 'Scientific American' in 1958.

**********

1962

In his 'Flexagons Inside Out', Les Pook refers to a 'comprehensive report, at the serious mathematics level, by Conrad and Hartline (1962) and goes on to give a link to a document which leads to a report called 'The Theory of the Flexagon' by A S Conrad (Hartline is not mentioned) published by RIAS (the Research Institute for Advanced Studies in Baltimore). This report was rescued from obscurity by Harold V McIntosh and states that it is 'A faithful reproduction of a RIAS Miscellaneous Publication of the same title, apparently later numbered RIAS Technical Report 60-24.' This report is mainly a discussion of the hexaflexagon family, but there is also a chapter on other flexagons which illustrates strips for a silverflexagon (and a bronze flexagon). Their properties are not, however, discussed.

The silverflexagon strip is 24 leaves long and certainly has many more than 6 faces. The Zigzag Silverflexagon, half its length, can be flexed into 12 flat states.

**********

1971

'The Combinatorial Richness of Folding a Piece of Paper' by Martin Gardner, an article published in 'Scientific American' of May 1971, contained instructions for making a paperfolding puzzle by William Dudeney and three others by Robert E Neale, two of which are flexagons, the Cross Flexagon (in its basic undecorated version) and the Sheep and Goats puzzle, which is based on the silverflexagon I call the Woven Flexatube. The solutions were published in the June 1971 issue.

As far as I know this is the first mention of the Sheep and Goats puzzle in the literature.

**********

1976

Peter Messer provides a reference to a chapter titled 'Flexagons for the Magician' in 'Paper Folding Geometry' by D A Johnson, published by J Weson Walch, 1976. I have not been able to access a copy of this book and so do not know what the article contains.

**********

1978

'Magic with Origami' by Ray Bolt, published as Booklet No 9 of the British Origami Society, probably in 1978, contains, inter alia, Robert E Neale's 'Sheep and Goats' puzzle.

**********

'Flexagons' by Paul Jackson, published as Booklet No 11 of the British Origami Society in 1978, contains, inter alia, two silverflexagons made from straight strips. One of these, made from a straight strip of silver triangles and titled here the Double Square Flexagon is the silverflexagon I call the Labyrinth Silverflexagon (although only a few of the many possible flexes are explained, and the author may not have been aware that many more existed). The other, made from a longer straight strip of silver triangles, is titled the Strip Flexagon. The author states that both are derived from 'Sheep and Goats' by Robert Neale.

As far as I know this is the first mention of the Labyrinth Silverflexagon in the literature.

**********

1988

'Build Your Own Polyhedra' by Peter Hilton and Jean Pederson, which was published by Addison-Wesley in 1988, contains a chapter titled 'Constructing Flexagons'. Inter alia, this chapter shows how to build and flex the Labyrinth Silverflexagon (called the 4-8-flexagon or tetra-octa-flexagon here), which is made from a straight strip 16 segments / leaves, and what is called the 8-8 flexagon, made from a straight strip of 32 segments / leaves. Although the author seems to be aware that they are more complicated only the simpler properties of these silverflexagons are discussed.

**********

1998

'The Magic of Flexagons' by David Mitchell, published by Tarquin publications in 1998, is a cut out and glue together book of flexagons and other flexible devices. Inter alia, it contains two silverflexagons, the Double Layer Flexitube (ie the Woven Flexitube) and the Harlequin Flexagon (aka the First Slit-Square Silverflexagon). This book replaced part of Tarquin's Mathematical Curiosities series and contains a mixture of the existing material from those booklets, some of my own inventions and additional explanatory material by Gerald Jenkins, the publisher. As far as I know this is the first publication of the First Slit-Square Silverflexagon.

**********

1999

'The Mathemagician and Pied Puzzler, a collection in tribute to Martin Gardner', edited by Elwyn Berkelkamp and Tom Rodgers, was published by - A R Peters in 1999. It contains a chapter titled 'Self-Designing Tetraflexagons' by Robert E Neale which considers various ways in which non-twisted flexagons can be constructed by removing areas from, or cutting slits into the centre of, a square. The designs explained are the Cross Flexagon, the Window Flexagon (two different versions with different properties), and several flexagons made from complete squares slit in various ways (which are not given names). The author notes that ' The first flexagon I saw that did not need glue (ie a non-twisted flexagon) was shown to me by Giuseppe Baggi years ago.' The context makes it clear that this is a reference to the Window Flexagon. This must have been in or prior to 1972 when Giuseppe Baggi died. The author also notes that the ms for this chapter was first submitted for publication in 1993 'but written more than a year or two before that.'

**********

'Silverflexagons 1' by David Mitchell, was privately published in 2002. It contains a full analysis and flexing maps of the Zigzag Silverflexagon (made from a zigzag strip of 12 right angle isosceles triangle segments / leaves) and the Woven Flexitube (made from the same strip but with the zigzags filled in). The strips for other related silverflexagons are given but their properties are not discussed.

**********

'Silverflexagons 2' by David Mitchell, was privately published in 2002. It contains a full analysis and maps of the First Slit-Square Silverflexagon, both versions of the related Non-Twisted Slit Square Flexagon and shows how the design can be generalised to create further flexagons from other polygons.

**********

'Silverflexagons 3' by David Mitchell, was privately published in 2002. It contains a full analysis and maps of the Labyrinth Silverflexagon (which is made from a straight strip of 16 right angle isosceles triangles) and has 228 separate flat states in all.

**********

2001

The First Slit-Square Silverflexagon appeared in Landelijke Oridag de Meern published by the OSN, the Netherlands origami society.

**********

2009

'Serious Fun with Flexagons' by Les Pook, published by Springer in 2009 Concentrates on edge ring flexagons made from polygons of various shapes from a solid mechanics linkage perspective and shows how silver flexagons and bronze flexagons relate to these designs.

**********

2011

The First Slit-Square Silverflexagon appeared in Orison 1 - 2011 published by the OSN, the Netherlands origami society.

**********

2015

'Silverflexagons and the Flexatube' by David Mitchell, was published by Water Trade publications in 2015. It contains all the information published in Silverflexagons 1, 2 and 3 and further information about the Flexatube puzzle.

**********