| Origami Heaven A paperfolding
paradise
The website of
writer and paperfolding designer David Mitchell
x
|
| |
| Nolids and Other Planar
Designs |
| |
| Nolids
are solids of no volume. They can be viewed as composed
of triangular sections of planes which run from the
centre of symmetry of a polyhedron to its edges. In
modular origami nolids paper modules replace and
represent these imaginary planes. Three of these nolids are
special cases in which the triangular planes line up to
form larger sections of planes that are polygonal in
shape. Viewed in this way, the nolid octahedron is
composed of three interpenetrating squares, the nolid
cuboctahedron of four interpenetrating hexagons and the
nolid icosidodecahedron of six interpenetrating decagons.
Similarly my Level
2 Three Colour Octahedral Pyramid can be seen as being
composed of six interpenetrating 2x1 rectangles and my 12
Interpenetrating Pentagonal Rings as being composed of,
well, the title says it all really!
|
| |
| |
| |
 |
|
Name: Robert Neale's
Octahedron, Skeletal Octahedron or
Nolid Octahedron (6-part) Modules / Paper
shape / Folding geometry: 6 modules from squares
using standard folding geometry.
Designer /
Date: Robert Neale, mid 1960s. Many other
paperfolders have independently originated this
design , including Kunihiko Kasahara, also in the
mid 1960's, slightly later than Robert Neale but
on the other side of the world, and Joe Power, in
Hawaii, sometime in the early to mid 1970's.
Incorrectly attributed to Seiryo Takegawa in
Origami Christmas Tree Decorations, Paul Jackson,
BOS booklet 20, 1982.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Nolid Octahedron
(2-part) Modules / Paper shape / Folding
geometry: 2 modules from squares using standard
folding geometry.
Designer /
Date: David Mitchell, 1988.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
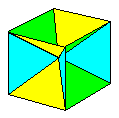
Name: Skeletal
Cube or Nolid Cube Modules / Paper
shape / Folding geometry: 12 modules from silver
rectangles .
Designer /
Date: David Brill, 1980s.
Diagrams:
In Mathematical Origami - David Mitchell -
Tarquin 1997 - ISBN 189961818X
|
|
| |
 |
|
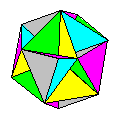
Name: Skeletal
Icosahedron or Nolid Icosahedron
- a development of David Brill's
Skeletal Cube arrived at by folding the modules
from golden rectangles rather than the silver
rectangles of the original design. Modules / Paper
shape / Folding geometry: 30 modules from golden
rectangles.
Designer /
Date: Kunihiko Kasahara, 1980s.
Diagrams: In
Kunihiko Kasahara and Toshie Takahama's 'Origami
for The Connoisseur' - Japan publications 1987 -
ISBN 0-87040-670-1.
|
|
| |
 |
|
Name: Nolid
Tetrahedron Modules / Paper
shape / Folding geometry: 6 modules from silver
rectangles.
Designer /
Date: David Mitchell, 1988 / Ian Harrison.
Diagrams:
Not yet available.
|
|
| |
 |
|
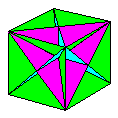
Name: Nolid
Cube with Two Nolid Tetrahedra Modules / Paper
shape / Folding geometry: Made by adding 30
modules, of two kinds, all folded from silver
rectangles, to David Brill's Nolid Cube.
Designer /
Date: David Mitchell, 2002. Based on a previous
design by Ian Harrison.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Six
Interpenetrating Planes in a Cube Modules / Paper
shape / Folding geometry: Made by adding 30
modules, of two kinds, all folded from silver
rectangles, to David Brill's Nolid Cube.
Designer /
Date: David Mitchell, 2002.
Diagrams:
Not yet available.
|
|
| |
 |
|
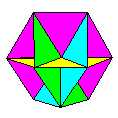
Name: Skeletal
Cuboctahedron (12-part) or Nolid
Cuboctahedron (12-part) Modules / Paper
shape / Folding geometry: 12 modules from squares
using 60/30 degree geometry.
Designer /
Date: Tung Ken Lam
Diagrams:
|
|
| |
 |
|
Name: Skeletal
Dodecahedron or Nolid
Dodecahedron Modules / Paper
shape / Folding geometry: 30 modules from squares
using standard folding geometry.
Designer /
Date: David Mitchell, 1988.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Nolid
Icosidodecahedron or Skeletal
Icosidodecahedron - can be conceived of
as composed of six interpenetrating decagons. Modules / Paper
shape / Folding geometry: 60 modules folded from
squares using mock platinum folding geometry.
Designer /
Date: David Mitchell, 1990.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Four
Octahedra - four Robert Neale Octahedra
linked with joining pieces from squares. Larger
versions are possible. . Modules / Paper
shape / Folding geometry: Each Robert Neale
Octahedron is made from 6 modules from squares
using standard folding geometry. Each joining
piece is from a square using standard folding
geometry.
Designer /
Date: David Mitchell, 2016. Update of work from
1995.
Diagrams:
In Building with Butterflies - David Mitchell -
Water Trade - ISBN 978-0-9534774-7-0.
|
|
| |
 |
|
Name: 12
Interpetrating Pentagonal Rings Modules / Paper
shape / Folding geometry: Developed from the
60-part Corner-pocket Sonobe Spiky Star by the
addition of 30 extra modules to link the vertexes
together into rings. All modules from squares
using standard folding geometry.
Designer /
Date: David Mitchell, 1995.
Diagrams:
Not yet available.
|
|
| |
| |











