An angular system is a system of related angles which are used to create an origami design.

A folding geometry is a method of creating an angular system.

Folding geometries are of three quite distinct kinds, natural, embedded and non-located. In the first two kinds of folding geometry the folds and/or creases are positioned by the use of location points. In the third kind the position of the folds and/or creases are positioned by eye (though their positions may subsequently be refined by an iterative process).

Two or more of these distinct types of folding geometry may be combined within a single design.

Primary and Secondary Folding Geometries

The primary folding geometry of a paper-shape is the folding geometry obtained by using just the primary reference points (the original edges and corners of the paper-shape) to determine where the creases will form.

In order to explain these concepts clearly we will first consider the simple case of the square.

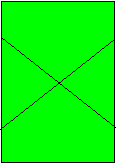
The primary folding geometry of the square consists of two creases obtained by folding opposite edges onto each other and two creases obtained by folding opposite corners onto each other. The first set divide the square into four smaller squares. The second set bisect these smaller squares at 45 degrees. The resulting crease pattern is familiar as the crease pattern of the waterbomb base and preliminary fold.

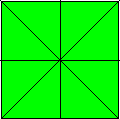
The primary folding geometry creates secondary reference points. In the case of the square these additional reference points are the four internal creases and the five points where the internal creases intersect each other and the edges of the square. These secondary reference points can be used to locate further creases, thus producing a secondary folding geometry.

For instance, the picture below shows the crease pattern of the bird base which can be obtained as a secondary folding geometry of the square.

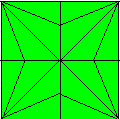
We can call this angular system the 90/45 degree system or simply standard folding geometry. The vast majority of origami designs folded from squares use this angular system.

Embedded Secondary Folding Geometries

An embedded folding geometry is a folding geometry obtained using secondary location points which would more naturally be obtained as the primary folding geometry of a different paper shape.

The most common example of the creation of an embedded secondary folding geometry is the way in which an angle of 60 degrees can be produced by folding two adjacent corners of a rectangle onto a crease obtained by folding the rectangle in half from edge to edge.

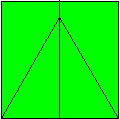
We can call this angular system the 60/30 degree system. It is natural to the bronze rectangle (and of course to the hexagon and equilateral triangle) but needs to be embedded in all other paper shapes.

The 60 degree system is the most commonly used embedded folding geometry.

Other Rectangles

The natural folding geometry of rectangles other than the square is more complex (and thus offers more interesting opportunities to the origami designer). The drawings below shows the grid of creases that can be obtained using the corners and edges of a typical oblong as location points.

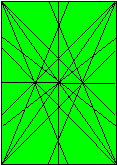
The usefulness of the natural folding geometry of a rectangle is largely determined by the angle at which the creases formed by folding opposite corners together cross (or the angle at which the diagonals cross - which is always the same).

Other Natural Angular Systems

There are clearly as many natural angular systems as there are rectangles to derive them from. However the most commonly used angular systems met in modular origami design are:

• The 90/45 degree system, or standard folding geometry, natural to any rectangle.

• The 120/60/30 degree system natural to the bronze rectangle, hexagon and equilateral triangle but also easily embedded in other rectangles.

• The 109.28/70.32/54.84/35.36 degree system natural to the silver rectangle but also easily embedded in squares and other rectangles.

• The 108/72/36 degree system natural to the twin platinum rectangles but most commonly found in modular origami in its approximated form as mock platinum folding geometry. Mock platinum folding geometry is derived from 1:3 rectangles but also easily embedded in squares and other rectangles.

• The 116.34/63.26 degree system natural to the golden rectangle but also easily embedded in other rectangles.

All angular systems natural to one particular rectangle can be embedded in any other rectangle (indeed in any other paper shape) by means of a careful choice of location points.

Non-located Folding Geometry

A non-located folding geometry is one where the folding geometry is not accurately located and is initially established by eye alone, by means of what is sometimes known as a 'right about there' fold.

This type of folding geometry is most commonly met in the method of dividing an edge or a crease into three (or five) roughly equal parts by means of a first guesstimate refined by an iterative process.

There are however a number of models where the whole folding geometry of the design depends on a 'right about there' non-located fold.