| Origami Heaven A paperfolding
paradise
The website of
writer and paperfolding designer David Mitchell
x
|
| |
| Modular Designs from
Bronze and Double Bronze Rectangles |
|
| |
| Bronze
rectangles are rectangles which have sides in the
proportion of 1:sqrt3. They naturally yield angles of 60
and 30 degrees. Double bronze rectangles are made by
laying two bronze rectangles together long edge to long
edge). Where
designs are not otherwise attributed they are my own.
|
| |
| Designs
from Bronze Rectangles |
| |
 |
|
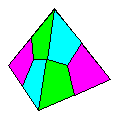
Terada
Modules, named after their creator,
Norishige Terada, are versatile modules folded
from bronze triangles that can be configured to
make numerous deltahedra such as the Double
Kite Pattern Tetrahedron pictured here,
which is made from 6 modules. I discovered that
it was possible to fold much simpler modules that
would make the same range of designs. When I
showed this module to Tomoko Fuse she told me it
was known as the Abe Module
(presumably after Hisashi Abe). I would be
grateful for any further information about this. |
|
| |
 |
|
The Modular Flip Flop
is my reconstruction of a design by the Danish
paperfolder Thoki Yenn which has become lost
(probably because Thoki abandoned it in favour of
his one piece version of the same design). The
design is a version of a well known mathematical
toy with the strange property that it will squash
flat in two different directions. Diagrams are not yet
available.
|
|
| |
 |
|
These two Cuboctahedra
(with sunken square faces) can both be
assembled from the same set of 4 modules. They
are both slightly flexible. Diagrams are not yet
available.
|
|
| |
 |
|
This Snub
Cube is also a 4-part design. If all the
creases of ghe modules were reversed they could
be assembled into the enantiomorphic form. Diagrams are not yet
available.
|
|
| |
 |
|
This 2-part
Truncated Tetrahedron is a delicate
design with sunken triangular faces. Four modules
of the same design can be assembled into a Truncated
Octahedron. Diagrams are not yet
available.
|
|
| |
 |
|
It is also possible
to fold modules from bronze rectangles that will
allow the construction of a 4-part
Truncated Tetrahedron with open
triangular faces. 8 modules of identical design
will go together to make a Truncated
Octahedron and 20 to make a Truncated
Icosahedron. Diagrams are not yet
available.
|
|
| |
 |
|
It is also possible
to create modules that will make a 6-part
Truncated Tetrahedron. Diagrams are not yet
available.
|
|
| |
 |
|
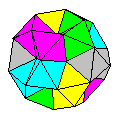
Modules folded from
bronze rectangles can also be used to make more
robust polyhedral designs such as this 10-part
Icosidodecahedron. Diagrams are not yet
available.
|
|
| |
| Designs
from Double Bronze Rectangles |
| |
 |
|
This is my 12-part Nolid
Cuboctahedron, from 1988, which can be
seen as consisting of four interpenetrating
hexagons. The original modules were folded from
hexagons, but they can equally well be folded
from squares or double bronze rectangles. Diagrams for modules
folded from double bronze rectangles can be found
in Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X.
|
|
| |
 |
|
I designed this 2-part
Tetrahedron, which is made by combining
mirror-image modules folded from double bronze
rectangles in 1988. Diagrams can be
found in Mathematical Origami - Tarquin
Publications - ISBN 1-899618-18-X.
|
|
| |
 |
|
Double bronze
rectangles can also be used to make corner-pocket
modules analogous to the Sonobe Corner-pocket
module, but folded using 60 degree geometry. 4 of
these modules will go together to create a robust
4-part Octahedron. Diagrams are not yet
available.
|
|
| |
 |
|
10 of the same type
of modules will also go together to create a
robust Icosahedron. Diagrams are not yet
available.
|
|
| |
| |











