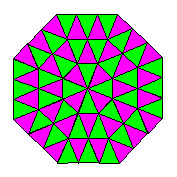
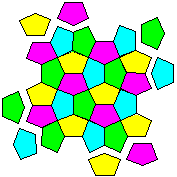
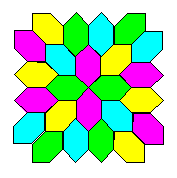
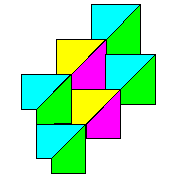Origami Heaven

A paperfolding paradise

The website of writer and paperfolding designer David Mitchell

x
 
About Origami Tiles and Tiling Patterns
 
Origami tiles are simple flat shapes that can be folded from ordinary photocopy paper and then laid together to create colourful tiling patterns. They are ideal for use in the mathematics classroom or at mathematics clubs.

Origami tiles can be used as the basis for investigations of angle, shape and symmetry. If they are unfolded back to their starting shape the crease patterns can easily be used to work out the angles (there is a worked example in the Trapezium tiles pdf). In some cases these crease patterns also reveal interesting relationships between the area or perimeter of the tile and the area or perimeter of the starting rectangle. Where I know of such a relationship I have added notes to the diagrams.

I have used these tiles in mathematics lessons with children ranging from 6 to 13 years of age and have found that children are quickly engaged by the activity of folding a number of tiles and working out the various ways in which they will go together. If the tiling pattern is to be glued onto a large sheet for display I would recommend getting each child to write their name on the tile(s) they have folded so that their contribution to the overall result is clear.

Many of these tiles are folded from 1:sqrt2 or silver rectangles. DIN paper sizes such as A4 or A5 etc are good enough approximations of this rectangle for classroom use. Since you can cut a silver rectangle into two half size silver rectangles they are easily scaled. DIN paper sizes are not easily available, however, in all countries, so I have also usually included a method of folding the same tile from the square. Some can also be folded from US letter size paper.

I have also included a number of methods of folding tiles from leftover rectangles, the 1:sqrt2+1 rectangle left over when the largest possible square is removed from a silver rectangle. This is partly because I often fold from squares cut from A4 paper and so usually have a large number of leftover rectangles lying around - and you may too! - and partly because the methods are often either extremely simple, mathematically interesting or both.

Origami tiles and tiling patterns can be very simple or quite complex to fold and lay together. In the details that follow the simplest tiles are listed first ... and the most difficult last.
 
 
 
  Trapezium Tiles - folded from silver rectangles and US letter sized paper. This is probably the simplest possible origami tile made with just one fold.

When folded from a silver rectangle the perimeter of this tile is 3 x sqrt2 ie three times the length of the long edge of the rectangle.
 
  Octagon Kite Tiles - folded from squares and silver rectangles.

When folded from a silver rectangle the perimeter of this tile is 4 ie four times the length of the shorter edge of the rectangle. The notes explain how several other shapes with perimeter 4 - two rectangles and two other tiles - can also be folded from the silver rectangle.

Octagon Kite tiles can also easily folded into Cairo tiles.
 
  Octagon Isosceles Tiles - folded from squares, silver rectangles and leftover rectangles.

When folded from a silver rectangle the area of this tile is half the area of the starting rectangle. The crease pattern can also be used to explain the formula for calculating the area of a triangle.
 
  Versatiles - folded from silver rectangles and squares.

When folded from a silver rectangle the area of the tile is half that of the starting rectangle.
 
  Octagon Rhombus Tiles - folded from squares, silver rectangles and leftover rectangles.
 
  Cairo Tiles - folded from squares, silver rectangles and leftover rectangles.
 
  Squashed Hexagon Tiles - folded from squares and silver rectangles.
 
  Sphinx Tiles - folded from leftover rectangles, or any similarly proportioned strip of paper.
 
  Octagram Kite Tiles - folded from squares, silver rectangles and 1:1+sqrt2/2 rectangles derived from the leftover rectangle.

The area of the octagram kite tile is half the square of the length of the long edge of the tile. When the tile is folded from a 1:1+sqrt2/2 rectangle this can be demonstrated by dissection and reassembly.
 
  Pentagonal Tiles - folded using angles approximated from squares and silver rectangles. The notes contrast the angles obtained from each paper shape and explain how the errors are distributed around the angles.
 
  Golden Proportion Tiles (aka Mountain and Molehill tiles) - folded using angles approximated from squares and silver rectangles. The notes contrast the angles obtained from each paper shape and explain how the errors are distributed around the angles.
 
  Penrose Kites and Darts - folded using angles approximated from 2 x 1 rectangles. Can be used to construct interesting periodic and non-periodic tiling patterns.