| Origami Heaven A paperfolding
paradise
The website of
writer and paperfolding designer David Mitchell
|
| |
|
| |
| An
assembly system is the way in which the modules
self-integrate to create the modular form. The analysis
presented on this page is neither complete nor
exhaustive. Modular designers often combine elements of
different assembly systems within the same design and are
always inventing new techniques. It is a common misconception
that modular designs are largely held together by
friction. In fact this is rarely the case.
|
| |
 |
|
Glue,
Tape and Thread Technically designs which are held
together by glue, tape or thread are multi-piece
glued. taped or threaded arrangements rather than
modular designs. For a more detailed explanation
of why this is see Definitions and
Notes. The picture to the left is of my
Spiky design which is a sticky note design held
together by the sticky part of the notes.
|
|
| |
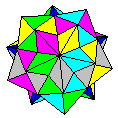
| Tab and Pocket
designs The most common assembly system
strategy used in modular origami design is to
supply each module with a set of tabs and
pockets, the tabs of one module being inserted
into the pocket of another during the assembly
process. The strengthy of the link between the
modules is commonly increased by by inserting the
tabs around the angle of a fold within the
pocket. The Sonobe module is the best known
example of a module of this kind.
|
|
 |
|
| |
 |
|
Wraparound
Weave designs In a wraparound weave system the
modules are arranged so that they wrap around (at
least part of) the outside of each other and so
hold each other in place. Good examples of this
type of design are the traditional 6-Card Cube
(shown to the left), David Brill's Waterbombic
Dodecahedron or my own 6-part Stellated Rhombic
Dodecahedron (in which the modules are themselves
three-dimensional forms).
|
|
| |
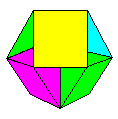
| Compact Weave
designs In a compact weave design the
modules are assembled so that part (normally
half) the module goes outside of, and part (yes,
normally the other half) inside of adjacent
modules. The stability of this assembly system
depends entirely on the overall shape of the
form. Some, like Paul Jackson's Cuboctahedron,
pictured right, are completely stable, while
others are very delicate structures indeed.
|
|
 |
|
| |
 |
|
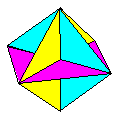
Self-tab-and-pocket
designs In some compact weave designs the
configuration in which the modules are held as a
result of the weave is such that parts of the
module are effectively formed into tabs and other
parts into sockets. This can be called a
self-tab-and-pocket system. Robert Neale's
Octahedron (pictured left) is the classic example
of this technique.
|
|
| |
| Mutual Compression This assembly system
trelies on the resilience of paper to
compression. Effectively, a part of each module
is compressed slightly by being inserted between
one of more adjacent modules, which in turn are
compressed by others etc. The resistance of the
paper to this compression locks the design
together. The best known example of a mutual
compression design is probanbly Paul jackson's
Cube (pictured right).
|
|
 |
|
| |
| |





