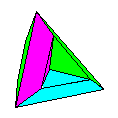| Origami Heaven A paperfolding
paradise
The website of
writer and paperfolding designer David Mitchell
x
|
| |
| A Classification of
Modular Forms |
|
| |
| The
categories into which modular forms are divided here are
not necessarily mutually exclusive. In addition other
modular forms exist which fall outside the scope of this
classification. Modular forms can also be divided into
finite and infinitely extensible forms, the latter being
structures that, in a theoretical sense at least, are
capable of being extended without limit in one or more
directions. In practice, of course, the limits of the
strength of the modules and their connection to each
other, the availability of sufficient paper, and perhaps
more importantly, of the folder's time and patience will
quickly be reached.
|
| |
| Non-Polyhedral
Forms |
| |
 |
|
Coasters,
Stars, Rotors and Rings These are the four
fundamental flat finite forms of modular origami.
Coasters
are simply flat polygonal forms, Stars are flat
forms with symmetrical points, Rotors flat forms
with assymetrical points and Rings are any of the
above with hollow centres. Complex Coasters are
sometimes called Mandalas. Rings are sometimes
called Wreaths. Removing one ore more modules
from these forms will often turn them into
dish-like forms.
The design
on the left is my 3-Fold Star, a minimalist
modular design.
|
|
| |
Quilts and Lattices
In origami a quilt is a form in
which modules are used to create a flat surface.
A Lattice is simply a quilt with holes in it.
Quilts and Lattices are usually infinitely
extendable forms but can, of course, be edged so
that they are finite forms instead.
The lattice on the right is an
unpublished design related to Windfarm.
|
|
 |
|
| |
 |
|
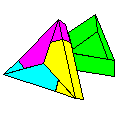
Containers Modular origami can
be used to make attractive open and lidded
containers of many shapes.
The
triangular lidded box pictured here is a design
by Tomoko Fuse.
|
|
| |
| Polyhedral
Forms |
| |
| Flat-faced forms Modular origami
provides an excellent way to model many Platonic,
Archimedean, Rhombic and other polyhedra. In
order to achieve a flat-faced design the geometry
of the modules must match (or at least closely
approximate) the geometry of the polyhedron being
modelled.
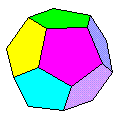
The design
shown to the right is my full-faced dodecahedron
from Mathematical Origami.
|
|
 |
|
| |
 |
|
Open-face
forms It
is sometimes possible to model a flat-faced
polyhedron in such a way that some of the faces
are entirely missing as in the case of this
truncated icosahedron design.
This is an
as yet unpublished design of my own.
|
|
| |
Pimpled forms
Pimpling of the faces of a
polyhedral model occurs when (because the
geometry of the modules does not match the
geometry of the underlying polyhedron) there is
too much paper to form a flat face and the excess
paper is configured to point outwards away from
the centre of symmetry of the design, thus
forming pimples (or pyramids) instead.
The form shown here is an 8-point
Stubby Star made from Sonobe modules. The
underlying polyhedron is an octahedron.
|
|
 |
|
| |
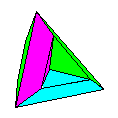 |
|
Dimpled
forms Conversely
dimpling occurs when the excess paper is
configured to point inwards towards the centre of
symmetry of the underlying polyhedron.
This
picture shows my Tricorne design which is a
dimpled silverhexahedron.
|
|
| |
Open-frame forms
An open-frame form is simply a
polyhedron with holes in the centre of the faces.
Forms of this kind are sometimes referred to as
pierced designs. Like unpierced forms open-frame
polyhedra may be flat-faced, pimpled or dimpled.
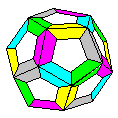
This design is an open-frame
dodecahedron from Mathematical Origami.
|
|
 |
|
|
 |
|
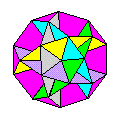
Nolids Nolids ( that is
solids of no volume) can be seen as polyhedra
whose faces have been dimpled to the point where
the apex of the dimple lies at the centre of
symmetry of the underlying polyhedron. They are
also sometimes referred to as skeletal or planar
designs, though the latter description may be
used of any design in which finite planes are
represented by layers of paper irrespective of
whether the design is a nolid or not.
This design
is my nolid icosidodecahedron.
|
|
| |
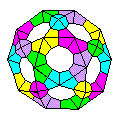
Hybrid forms
It is frequently possible to combine
many of these modelling tecxhniques withi a
single design. This design, for instance, is my
Proteus sculpture which has flat triangular faces
combined with open-frame dimpled pentagonal ones.
|
|
 |
|
| |
 |
|
Surface
Analogues The surface of many polyhedra can be
distorted (by folding) to create forms that look
entirely different but are nevertheless in
modular origami terms closely related designs.
The design
shown to the left is my 6-part Enigma Cube which
is an analogue of the cube and is made by
altering the way in which the six simple modules
that are used to make a Blintz Cube are
configured without altering their relationship to
each other within the finished modular assembly.
|
|
| |
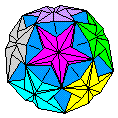
Sculptural forms
Any of these types of polyhedral
forms can be augmented with additional flaps,
extra modules etc to create forms that, while
based on the form of an underlying polyhedron,
are in final appearance more akin to decorative
ornaments or sculpture.
Forms of this kind which resemble a
ball of flowers are known as kusudama.
|
|
 |
|
| |
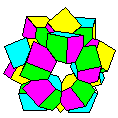 |
|
Polyhedral
Combinations Modular designs can also be created
by combining several, or many, basic polyhedral
forms to produce a more complex form. Sometimes
this kind of modular structure is not valid
mathematically, but works in terms of modular
origami because the inaccuracies are small enough
to be absorbed in the assembly process.
My 20-Cubes
design pictured here is a good example of such an
unmathematical form.
|
|
| |
| Modular Action Designs |
| |
Modular Action Designs
Modular designs are not necessarily
rigid. Many can be manipulated to change the
relationship of the parts to each other. Modules
may rotate or slide into different positions, the
whole design my rotate through its centre of
symmetry or it may collapse flat in one or
several directions. The possibilities for such
designs are probably unlimited.
The design shown here is my Rotating
Ring of Rhombic Polyhedra from Mathematical
Origami.
|
|
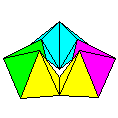 |
|
| |
| Macromodular Forms |
| |
 |
|
Stacks,
Walls, Forests and Pyramids Stacks (or towers)
are macromodular structures in which the
macromodules sit directly on top of each other.
They may be held together by joining-pieces or
just by gravity. Walls are formed by connecting
or arranging several stacks in a linear fashion,
forests by connecting them into larger non-linear
groups. Pyramids are formed where the
macromodules are not stacked directly on top of
each other. Pyramids may also be linear or
non-linear in form.
The picture
shows a forest of my Columbus Cubes.
|
|
| |
Macromodular Lattices
In contrast to stacks and pyramids
macro-modular lattices are structures that are
firmly linked together in all directions. Many
lattices have open spaces within the structure
but that is not a necessary defining
characteristic.
The picture to the right shows my
Borromean Lattice design.
|
|
 |
|
| |
 |
|
Nested
Macromodular forms Nested forms can be created by
building several complete modular polyhedral
structures inside each other. In this case a
solid tetrahedron nestles inside an open-frame
cube which in turn sits within an open-frame
dodecahedron.
Tomoko Fuse
has published several designs for structures of
this kind.
|
|
| |
Interwoven Macromodular Forms
Forms of this type can be created by
linking several (or many) open-frame modular
polyhedral designs to and through each other.
The design shown here is Tom Hull's
Five Intersecting Tetrahedra. The open-frame
tetrahedra which Tom has used as macromodules are
a design by Francis Ow.
|
|
 |
|
| |
| |