| Origami Heaven A paperfolding
paradise
The website of
writer and paperfolding designer David Mitchell
|
| |
| 2-part
Modular Designs |
| |
| Flat
Designs |
| |
 |
|
Name: A Marriage of
Opposites Modules / Paper shape / Folding
geometry: 2 mirror-image Maverick modules from
squares using standard folding geometry.
Designer /
Date: Tomoko Fuse, 1980s. David Mitchell, 1990.
Different folding method, same result.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Star of David Modules / Paper
shape / Folding geometry: 2 modules from
equilateral triangles using 120/60 folding
geometry.
Designer /
Date: Lewis Simon, possibly 1970s..
Diagrams:
In Origami Christmas Tree Decorations, Paul
Jackson, BOS booklet 20, 1982.
|
|
| |
 |
|
Name: Ring of 8 Squares Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: Wayne Brown, c1982.
Diagrams:
In Origami Christmas Tree Decorations, Paul
Jackson, BOS booklet 20, 1982.
|
|
| |
| 3D
Designs |
| |
 |
|
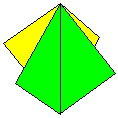
Name: The Preliminary
Ornament is made by the simple expedient
of weaving together two Preliminary Folds. Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: The earliest publication of this design
that I know of is in The Origamian Vol 7 Issue 4
of Winter 1967 where it is called Tree Ornament
and attributed to Molly Kahn.
Diagrams:
On-line diagrams are available in the Cushions
pdf on the Modular Designs page of this site.
|
|
| |
 |
|
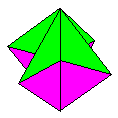
Name: The Spinner,
originally a hanging ornament but also makes an
excellent wind-top if held between the palms and
blown at gently. Modules / Paper shape / Folding
geometry: 2 modules from squares using standard
folding geometry.
Designer /
Date: Attributed to Alice Gray in Paul Jackson's
'Origami Christmas Tree Decorations', British
Origami Society booklet 20 published in 1982,
although it is clearly a simple variation of
Molly Kahn's Preliminary Ornament. I do not know
who first discovered it would function as a
spinning toy.
Diagrams:
Presented as an ornament - in Paul Jackson's
Origami Christmas Tree Decorations - British
Origami Society booklet 20 - 1982. Presented as
an action toy - in Origami - David Mitchell -
Barnes and Noble 2002 - ISBN 0-7607-3331-7.
|
|
| |
 |
|
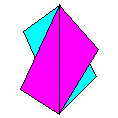
Name: The Oblong Ornament is
a version of the Preliminary Ornament that can be
made from any two identical oblongs. Modules / Paper
shape / Folding geometry: 2 modules from any
rectangle.
Designer /
Date: David Mitchell, 1993.
Diagrams:
On-line diagrams are available in the Cushions
pdf on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Molly Kahn's Tree
Ornament aka Fluted Diamond Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: Molly Kahn, 1967.
Diagrams:
In The Origamian Vol 7 Issue 4 of Winter 1967.
Diagrams also in Origami Christmas Tree
Decorations, Paul Jackson, BOS booklet 20, 1982.
|
|
| |
 |
|
Name: Robert Neale's 2-part
Octahedron - a classic design that is a
true joy to fold and assemble. Will collapse flat
and pop back into shape. Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: Robert Neale, 1968.
Diagrams:
As Octohedron In The Origamian Vol 8 Issue 3 of
Winter 1968.
|
|
| |
 |
|
Name: The Embroidered Ball aka
the Skillman Ball has the
interesting property that it can be squashed flat
in two directions, although this property does
not appear to have been known or appreciated at
the time of its first publication. Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: Jack J Skillman, c1969..
Diagrams:
In Flapping Bird magazine no 4, 1969. Also in
More Origami: The Art of Paperfolding No 2 in
1971 and Origami Christmas Tree Decorations, Paul
Jackson, BOS booklet 20, 1982.
|
|
| |
 |
|
Name: 2-part Decoration Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: David Mitchell, 1989. Has also been
independently discovered by Tung Ken Lam who
realised it will squash flat in two directions,
thus turning a rather ordinary paperfold into a
charming toy. On seeing this I realised that the
Skillman Ball will also squash flat, something I
had previously not been aware of.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Nordquist's Ornament Modules / Paper
shape / Folding geometry: 2 modules from 2x3
rectangles using standard folding geometry.
Designer /
Date: John M Nordquist, c1963.
Diagrams:
In Samuel Randlett's The Best of Origami, Faber
and Faber, 1964.
|
|
| |
 |
|
Name: Nordquist's Ornament
(from squares) - the first known nolid
octahedron design - aka Two-Piece
Octahedron Skeleton. Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: John M Nordquist, c1963.
Diagrams:
Photo and description only in The Best of
Origami, Samuel Randlett, Faber and Faber, 1964.
Diagrams in 3-D Geometric Origami, Gurkewitz and
Arnstein, Dover, 1995 where the design is called
the Two-Piece Octahedron Skeleton and attributed
to Bennett Arnstein.
|
|
| |
 |
|
Name: Nolid Octahedron
(2-part) - same form as Nordquist's
Ornament (from squares) but different modular
method. Modules / Paper shape / Folding
geometry: 2 modules from squares using standard
folding geometry.
Designer /
Date: David Mitchell, 1988.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
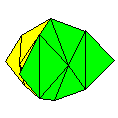
Name: UFO aka
4x4 Cushion Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: Paulo Mulatinho, c1998.
Diagrams:
First published in Paulo Mulatinho's Origami Neue
Ideen in 1998. On-line diagrams are available in
the Cushions pdf on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Cushions are
a series of 2-part designs from squares and other
rectangles developed from Molly Kahn's
Preliminary Ornament and the Oblong Ornament. Modules / Paper
shape / Folding geometry: 2 modules from any
rectangle.
Designer /
Date: In 2004, soon after seeing Paulo
Mulatinho's UFO, I realised the same idea could
be applied to larger grids and other rectangles.
In 2005 Tung Ken Lam realised that the divisions
of the grids need not be uniform.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: The Tsak-man / Hosoya
Cube Modules / Paper shape / Folding
geometry: 2 modules from squares using standard
folding geometry.
Designer /
Date: Ho Tsak-man, c1974 / Haruo Hosoya, c1987.
Diagrams:
Ho Tsak-man's cube can be found in The Flapping
Bird issue 20 1974. Haruo Hosoya's cube can be
found in Kunihiko Kasahara and Toshie Takahama's
'Origami for The Connoisseur' - Japan
publications 1987 - ISBN 0-87040-670-1.
|
|
| |
 |
|
Name: The 2-part Cube. Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: David Mitchell, 2006.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Simple Tetrahedra -
tetrahedral versions of the Business Card Cube
design. Modules / Paper shape / Folding
geometry: 2 mirror-image modules from squares (as
in picture) or any other rectangles using various
folding geometries.
Designer /
Date: David Mitchell, 2016. Design similar to,
but not consciously based on a design for a tree
Ornament by Molly Kahn in The Origamian Vol 7
Issue 4 of Winter 1967.
Diagrams:
Not yet available.
|
|
| |
 |
|
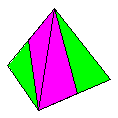
Name: Mirror-Image
Tetrahedron Modules / Paper
shape / Folding geometry: 2 mirror-image modules
/ Can be folded from many paper shapes. 60/30
degree folding geometry.
Designer /
Date: David Mitchell, 1997.
Diagrams:
From double-bronze rectangles in Mathematical
Origami - Tarquin Publications - ISBN
1-899618-18-X.
|
|
| |
 |
|
Name: Striped Mirror-Image
Tetrahedron Modules / Paper
shape / Folding geometry: 2 mirror-image Abe or
Terada modules or the equivalent geometry
embedded in squares. 60/30 degree folding
geometry.
Designer /
Date: David Mitchell, 2003.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: The Mirror-Image
Rhombic Tetrahedron Modules / Paper
shape / Folding geometry: 2 mirror-image modules
folded from silver rectangles.
Designer /
Date: David Mitchell, 1996.
Diagrams:
In Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X.
|
|
| |
 |
|
Name: The Rhombic
Tetrahedron (2-part) - three versions
possible as the set of modules can be configured
and assembled in three different ways. Modules / Paper
shape / Folding geometry: 2 modules folded from
double silver rectangle strips. Also possible,
but less successful, from truncated Nick Robinson
Rhombic modules folded from silver rectangles.
Designer /
Date: David Mitchell, 2017.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: The Lesser Rhombic
Tetrahedron Modules / Paper
shape / Folding geometry: 2 modules folded from
silver rectangles.
Designer /
Date: David Mitchell, 2017.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Truncated Tetrahedron
(2-part) - a large proportion of the
surface of this consists of just a single layer
of paper, yet the design is stable, rigid and
reasonably strong. Modules / Paper
shape / Folding geometry: 2 modules from bronze
rectangles using 60/30 degree folding geometry.
Designer /
Date: David Mitchell, 2000.
Diagrams:
Not yet available.
|
|
| |
 |
|
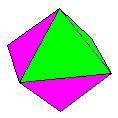
Name: The (Rhombus
Base) Rhombic Pyramid (2-part) Modules / Paper
shape / Folding geometry: 4 modules from silver
rectangles.
Designer /
Date: David Mitchell, 2000.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Octahedron (2-part)
- a delicate design probably best made from light
card. Modules
/ Paper shape / Folding geometry: 2 modules from
double bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 1997.
Diagrams:
In Mathematical Origami - Tarquin Publications -
ISBN 1-899618-18-X.
|
|
| |
 |
|
Name: Binary Modules / Paper
shape / Folding geometry: 2 modules from squares
using various folding geometries.
Designer /
Date: David Mitchell, 1988.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Binary 2 Modules / Paper
shape / Folding geometry: 2 modules from stars of
David using 60/30 degree folding geometry.
Designer /
Date: David Mitchell, 2008.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Thingamy Modules / Paper
shape / Folding geometry: 2 modules from silver
rectangles.
Designer /
Date: David Mitchell, 1990.
Diagrams:
On-line diagrams are available on the Modular Designs page of this site.
|
|
| |
 |
|
Name: Pinwheel Cubes -
series of winged cubes conceived of as a modular
assembly challenge. Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: David Mitchell, 1999.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: Enigma Cube (2-part) Modules / Paper
shape / Folding geometry: 2 modules from squares
using standard folding geometry.
Designer /
Date: David Mitchell, 1988.
Diagrams:
In Paper Crystals (2nd Edition) - Water Trade -
ISBN 978-0-9534774-9-4.
|
|
| |
 |
|
Name: The Modular Flip Flop
is my reconstruction of a design by the Danish
paperfolder Thoki Yenn which has become lost
(probably because Thoki abandoned it in favour of
his one piece version of the same design). The
design is a version of a well known mathematical
toy with the strange property that it will squash
flat in two different directions. Modules / Paper
shape / Folding geometry: 2 modules folded from
double bronze rectangles using 60/30 degree
folding geometry.
Designer /
Date: David Mitchell, 1989.
Diagrams:
Not yet available.
|
|
| |
 |
|
Name: (Modular) 2-Way Tube
- a modular version of Robert Neale's 2-Way Tube
(which can be made (in several ways) from a
single sheet of paper or light card). Modules / Paper
shape / Folding geometry: 2 modules from any
rectangle using standard folding geometry.
Designer /
Date: David Mitchell, 1997.
Diagrams:
On-line diagrams are available on the Devious Devices page of this site.
|
|
| |
| |